题目内容
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
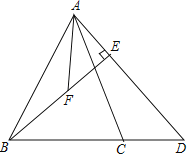
【答案】(1)![]() ;(2)9;(3)见详解
;(2)9;(3)见详解
【解析】
(1)在Rt△AEB中,利用勾股定理即可解决问题;
(2)由∠D=45°可证得BE=DE,再利用三角的面积公式计算即可;
(3)如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MFB,再证明△ABM≌△ACD即可.
(1)解:∵AB=AC,AC=![]() ,
,
∴AB=![]() ,
,
∵BE⊥AD,AE=![]() ,
,
∴在Rt△AEB中,![]() ;
;
(2)解:∵BE⊥AD,∠D=45°,
∴∠EBD=∠D =45°,
∴BE=DE=![]() ,
,
∴AD=AE+DE=![]() ,
,
∴![]() ;
;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
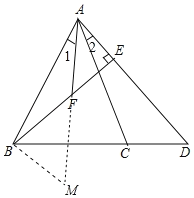
∵点F为BE的中点,
∴EF=BF,
在△AEF和△MBF中,
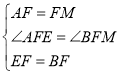
∴△AEF≌△MBF(SAS),
∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.
又∵∠BAC=∠DAF,
∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,
∴∠1=∠2.
在△ABM和△ACD中,
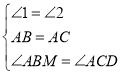 ,
,
∴△ABM≌△ACD(ASA),
∴AM=AD,
又∵AM=AF+MF=2AF,
∴2AF=AD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目