题目内容
【题目】(1)如图1,已知A、B两个边长不相等的正方形纸片并排放置,若m7,n3,试求A、B两个正方形纸片的面积之和.
(2)如图1,用m、n表示A、B两个正方形纸片的面积之和为 .(请直接写出答案)
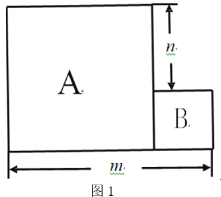
(3)如图2,若A、B两个正方形纸片的面积之和为5,且图2中阴影部分的面积为2,试求m、n的值.

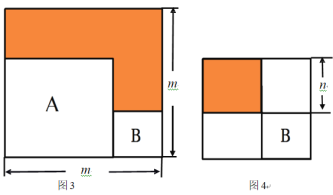
(4)现将正方形纸片A、B并排放置后构造新的正方形得图3,将正方形纸片B放在正方形纸片A的内部得图4,若图3和图4中阴影部分的面积分别为12和1,则A、B两个正方形纸片的面积之和为 .
【答案】(1)29;(2)![]() ;(3)3,1;(4)13
;(3)3,1;(4)13
【解析】
(1) 设正方形![]() 纸片边长为
纸片边长为![]() ,正方形
,正方形![]() 纸片边长为
纸片边长为![]() ,根据图形的特点列出二元一次方程组求出边长,即可求解;
,根据图形的特点列出二元一次方程组求出边长,即可求解;
(2)设甲、乙两个正方形纸片的边长分别为x,y,根据图形的特点列出二元一次方程组求出边长,即可解决问题;
(3)解:设正方形![]() 纸片边长为
纸片边长为![]() ,正方形
,正方形![]() 纸片边长为
纸片边长为![]() ,根据图形的特点列出方程组,从而求出大正方形的面积与小正方形的面积,得到其边长;
,根据图形的特点列出方程组,从而求出大正方形的面积与小正方形的面积,得到其边长;
(4)设正方形C、D的边长为c、d,由图4得:(cd)2=1,由图3得:(c+d)2c2d2=12,然后两个方程组合可得c2+d2的值.
(1)解:设正方形![]() 纸片边长为
纸片边长为![]() ,正方形
,正方形![]() 纸片边长为
纸片边长为![]() .
.
则![]()
解之得:![]()
所以,![]()
![]()
答:![]() 、
、![]() 两个正方形纸片得面积之和为
两个正方形纸片得面积之和为![]() .
.
(2)设甲、乙两个正方形纸片的边长分别为x,y;
由题意![]() ,
,
解得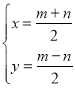
∴![]()
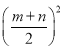 +
+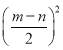 =
=![]()
(3)解:设正方形![]() 纸片边长为
纸片边长为![]() ,正方形
,正方形![]() 纸片边长为
纸片边长为![]() .
.
则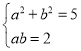
![]()
![]()
![]()
又![]() ,
,![]()
![]()
![]()
![]()
又![]() ,
,
![]()
(4)设正方形A、B的边长为c、d,则:
由图4得:(cd)2=1,即:c22cd+d2=1,
由图3得:(c+d)2c2d2=12,即2dc=12,
∴c2+d212=1,
∴c2+d2=13,
即正方形A、B的面积和为13.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某快车的计费规则如表1,小明几次乘坐快车的情况如表2,请仔细观察分析表格解答以下问题:
(1)填空:a= ,b= ;
(2)列方程求解表1中的x;
(3)小明的爸爸23:10打快车从机场回家,快车行驶的平均速度是100公里/小时,到家后小明爸爸支付车费603元,请问机场到小明家的路程是多少公里?(用方程解决此问题)
表1:某快车的计费规则
里程费(元/公里) | 时长费(元/分钟) | 远途费(元/公里) | |||
5:00﹣23:00 | a | 9:00﹣18:00 | x | 12公里及以下 | 0 |
23:00﹣次日5:00 | 3.2 | 18:00﹣次日9:00 | 0.5 | 超出12公里的部分 | 1.6 |
(说明:总费用=里程费+时长费+远途费)
表2:小明几次乘坐快车信息
上车时间 | 里程(公里) | 时长(分钟) | 远途费(元) | 总费用(元) |
7:30 | 5 | 5 | 0 | 13.5 |
10:05 | 20 | 18 | 66.7 |