Question

【题目】如图，在△ABC中，CE为三角形的角平分线，AD⊥CE于点F交BC于点D

(1) 若∠BAC＝96°，∠B＝28°，直接写出∠BAD＝__________°

(2) 若∠ACB＝2∠B

① 求证：AB＝2CF

② 若EF＝2，CF＝5，直接写出＝__________

Answer 1

【答案】（1）34°；（2）①见解析，②

【解析】

（1）在△ABC中，利用内角和可算出∠ACB，再由CE⊥AD，CE平分∠ACD，根据三线合一，可知△CAD为等腰三角形，即可求出底角∠CAD，进而求出∠BAD；

（2）①过A作AH∥BC，交CE的延长线于H，易得AH=AC，再由AD⊥CE，可得AD垂直平分CH，则CH=2CF，在由CH=CE+EH=BE+EH，而AE=EH，进而可得CH=BE+AE=AB，所以AB=2CF.

②易证△AHF≌△DCF，可得AH=CD，再由△AEH∽△BEH，得出相似比，进而得到.

解：（1）在△ABC中，

∵CE⊥AD，CE平分∠ACD

∴△CAD为等腰三角形，CA=CD

∴

∴

（2）①如图所示，过A作AH∥BC，交CE的延长线于H，

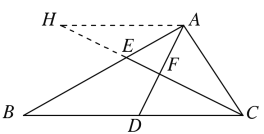
∵AH∥BC，∴∠H=∠BCE，∠B=∠BAH

又∵CH平分∠ACB，则∠ACH=∠BCH

∴∠H=∠ACH，∴AC=AH

又∵AF⊥CE，∴AD垂直平分CH，

∴CH=2CF

∵∠ACB＝2∠B，∴∠B=∠BCE，∴BE=CE

又∵∠B=∠BAH，∴∠H=∠BAH，∴AE=HE

∴CH=CE+EH=BE+AE=AB

又∵CH=2CF

∴AB=2CF

②在△AHF和△DCF中，

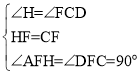
∴△AHF≌△DCF（ASA）

∴AH=CD

∵EF＝2，CF＝5，由①得BE=CE=CF+EF=7，AE=EH=HF-EF=5-2=3

又∵AH∥BC，∴，

∴，∴