题目内容
【题目】如图,已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是CB延长线上一点,且∠DEC=∠DCE,F是AC上一点且DF∥BC,若∠A=60°.
求证:EB=AD.

【答案】证明见解析
【解析】
由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论.
∵DF∥BC,∴∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE.
∵△ABC是等腰三角形,∠A=60°,∴△ABC是等边三角形,∴∠ABC=∠ACB=60°,∴∠DBE=120°,∠ADF=∠AFD=60°=∠A,∴△ADF是等边三角形,∠DFC=120°,∴AD=DF.
∵∠DEC=∠DCE,∴∠FDC=∠DEC,ED=CD.
在△DBE和△CFD中,∵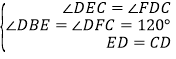 ,∴△DBE≌△CFD(AAS),∴EB=DF,∴EB=AD.
,∴△DBE≌△CFD(AAS),∴EB=DF,∴EB=AD.

练习册系列答案
相关题目






