Question

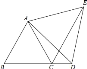
【题目】△ABC，△DEC均为直角三角形，B，C，E三点在一条直线上，过D作DM⊥AC于M．

（1）如图1，若△ABC≌△DEC，且AB=2BC．

①过B作BN⊥AC于N，则线段AN，BN，MN之间的数量关系为：　 　；（直接写出答案）

②连接ME，求的值；

（2）如图2，若AB=CE=DE，DM=2，MC=1，求ME的长．

Answer 1

【答案】（1）①AN﹣BN=MN；②；（2） .

【解析】

（1）①由题意先证得四边形ABED是正方形，再通过“角角边”证明△ABN≌△DAM，即AM=BN，则AN﹣BN=AN﹣AM= MN；

②连接ME，求的值；

（2）如图2，过E作EG⊥DM于G，EH⊥AC于H，过C作CF⊥ME于F，通过“角角边”证得△CEH≌△DEG，即GE=HE，则四边形MHEG是正方形，所以∠CMF=45°，在Rt△CFM中求得CF=MF=，在Rt△CDM中求得CD=，Rt△CEF中求得EF=，然后用MF+EF即可得解.

（1）①如图1，连接AD，

∵△ABC≌△DEC，

∴AB=2BC=2CE=BE，

又∵∠ABC=∠DEC=90°，

∴AB∥DE，

∴四边形ABED是正方形，

∴AD=BE=AB，∠BAD=90°，

又∵BN⊥AC，DM⊥AC，

∴∠DMA=∠ANB=90°，∠BAN+∠DAM=∠ADM+∠DAM=90°，

∴∠BAN=∠ADM，

∴△ABN≌△DAM（AAS），

∴AM=BN，

∵AN﹣AM=MN，

∴AN﹣BN=MN，

故答案为：AN﹣BN=MN；

②如图，延长AC，交DE的延长线于F，

由∠ABC=∠FEC=90°，BC=EC，∠ACB=∠FCE，可得△ABC≌△FEC，

∴EF=AB=DE，

∴E是DF的中点，

又∵∠DMF=90°，

∴Rt△DMF中，ME=DF=DE，

又∵CE=BE=DE，

∴=；

（2）如图2，过E作EG⊥DM于G，EH⊥AC于H，过C作CF⊥ME于F，

则∠DGE=∠H=90°，

∴∠HEG=90°=∠CED，

∴∠CEH=∠DEG，

又∵CE=DE，

∴△CEH≌△DEG（AAS），

∴GE=HE，

∴四边形MHEG是正方形，

∴∠CMF=45°，

∵MC=1，

∴CF=MF=，

在Rt△CDM中，CD=，

∴CE=DE=，

又∵Rt△CEF中，EF==，

∴ME=MF+EF=．