题目内容
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

【答案】OM=15米;MN=2米.
【解析】
作AE⊥OM,BF⊥OM,首先得出△AOE≌△OBF(AAS),进而得出CD的长,进而求出OM,MN的长即可.
解:
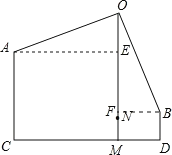
作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=![]() ,
,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
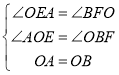 ,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m),
∵EF=EMFM=ACBD=103=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m,
又因为由勾股定理得ON=OA=13,
所以MN=1513=2(m).
答:旗杆的高度OM为15米,玛丽在荡绳索过程中离地面的最低点的高度MN为2米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







