��Ŀ����
����Ŀ����1����ͼ��1������֪��ABC,��AB��ACΪ������ABC�����ȱ�������ABD�͵ȱ�������ACE������BE��CD.�������ͼ�Σ���֤����BE=CD;

��2����ͼ��2������֪��ABC,��AB��ACΪ��������������ABFD��������ACGE,����BE��CD,BE��CD��ʲô������ϵ��˵�����ɣ�
��3������(1)(2)����������۵ľ����֪ʶ��������⣺��ͼ��3����Ҫ������������Ե�����B��E�ľ��룬�Ѿ���á�ABC=45�㣬��CAE=90�㣬AB=BC=1ǧ�ף�AC=AE.��BE�ij�.
���𰸡���1�������������2��BE=CD����3��![]() ǧ��
ǧ��
��������
��1�����õȱ������ε����ʣ��ñ߽DZ���֤��CAD�ա�EAB�����ɵ�BE=CD;
��2��֤��ͬ��1�����ñ߽DZ���֤��CAD�ա�EAB���ɵý����
��3���ɣ�1������2���Ľ��⾭���֪����A������ֱ��������ABD������CD�����ù��ɶ������BD��������õ���DBCΪֱ�������Σ����ù��ɶ������CD����ΪBE�ij�.
�⣺��1���ߡ�ABD����ACE���ǵȱ������Σ�
��AD=AB��AC=AE����BAD=��CAE=60��.
���BAD+��BAC=��CAE+��BAC��
�� ��CAD=��EAB.
����CAD����EAB��

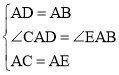 ��
��
���CAD�ա�EAB��SAS��. ��BE=CD
��2��BE=CD
����ͬ��1�������ı���ABFD��ACGE��Ϊ�����Σ�
��AD=AB��AC=AE����BAD=��CAE=90��.���CAD=��EAB.
������CAD����EAB��
AD=AB����CAD=��EAB��AC=AE
���CAD�ա�EAB��SAS������BE=CD
��3���ɣ�1������2���Ľ��⾭���֪����A������ֱ��������ABD����BAD=90��������CD��
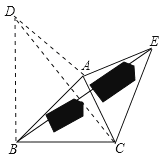
��AD=AB=1ǧ�ף���ABD=45������![]() ǧ��.
ǧ��.
����CD�����ɣ�2���ɵ�BE=CD.
�ߡ�ABC=45�������DBC=90��.
��Rt��DBC�У�BC=1ǧ�ף�![]() ǧ�ף�
ǧ�ף�
���ݹ��ɶ����ã�![]() ��ǧ�ף�.
��ǧ�ף�.
��BE=CD=![]() ǧ��.
ǧ��.








