题目内容
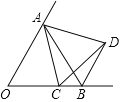
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积. 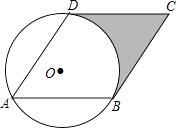
【答案】
(1)证明:连结OB、OD、OC,
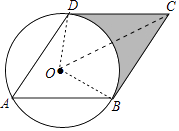
∵ABCD是菱形,
∴CD=CB,
∵OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠ODC=∠OBC,
∵CD与⊙O相切,∴OD⊥CD,
∴∠OBC=∠ODC=90°,
即OB⊥BC,点B在⊙O上,
∴BC与⊙O相切.
(2)解:∵ABCD是菱形,
∴∠A=∠DCB,
∵∠DOB与∠A所对的弧都是 ![]() ,
,
∴∠DOB=2∠A,
由(1)知∠DOB+∠C=180°,
∴∠DOB=120°,∠DOC=60°,
∵OD=1,∴OC=2,DC= ![]()
∴S阴影=2S△DOC﹣S扇形OBD=2× ![]() ×1×
×1× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连结OB、OD、OC,只要证明△OCD≌△OCB,推出∠ODC=∠OBC,由CD与⊙O相切推出OD⊥CD,推出∠OBC=∠ODC=90°,由此即可证明;(2)根据S阴影=2S△DOC﹣S扇形OBD计算即可;
【考点精析】通过灵活运用菱形的性质和扇形面积计算公式,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目