题目内容
【题目】如图，在△ABO中，已知点 
、B（﹣1，﹣1）、O（0，0），正比例函数y=﹣x图象是直线l，直线AC∥x轴交直线l与点C． 
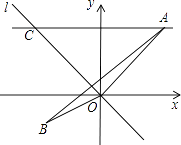
（1）C点的坐标为；
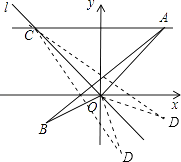
（2）以点O为旋转中心，将△ABO顺时针旋转角α（90°≤α＜180°），使得点B落在直线l上的对应点为B′，点A的对应点为A′，得到△A′OB′． ①∠α=；②画出△A′OB′．
（3）写出所有满足△DOC∽△AOB的点D的坐标．
【答案】
（1）（﹣3，3）
（2）90°
（3）解：∵A点坐标可知OA与x轴正半轴夹角为60°，可知∠AOB=165°，
根据对应关系，则∠DOC=165°，故OD在第四象限，与x轴正半轴夹角为30°或与y轴负半轴夹角为30°，
根据A、B、C三点坐标，
∴OA=2 
、OB= 
、OC=3 ，
∵ 
，
∴DO= 
= 
=6 ，
∴D点的横坐标为：3 ，或纵坐标为：﹣3 ，
∴D点坐标为（9，﹣3 ），（3 ，﹣9）．
【解析】解：（1）∵直线AC∥x轴交直线l于点C， ∴A、C两点纵坐标为3，代入直线y=﹣x中，得C点横坐标为﹣3，
∴C（﹣3，3）；（2）由B（﹣1，﹣1）可知，OB为第三象限角平分线，
又直线l为二、四象限角平分线，
∴旋转角为∠α=∠BOB′=90°，△A′OB′如图所示；
【考点精析】关于本题考查的一次函数的性质和相似三角形的判定与性质，需要了解一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．
练习册系列答案
相关题目
