Question

【题目】已知：在⊙O中，弦AC⊥弦BD，垂足为H，连接BC，过点D作DE⊥BC于点E，DE交AC于点F．

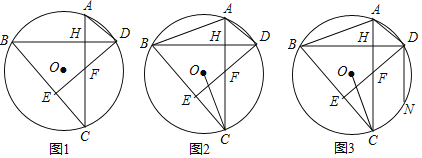
（1）如图1，求证：BD平分∠ADF；

（2）如图2，连接OC，若AC＝BC，求证：OC平分∠ACB；

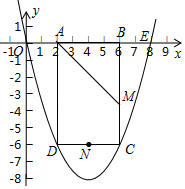
（3）如图3，在（2）的条件下，连接AB，过点D作DN∥AC交⊙O于点N，若AB＝3，DN＝9．求sin∠ADB的值．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）sin∠ADB的值为．

【解析】

(1)根据等角的余角相等即可证明；

(2)连接OA、OB．只要证明△OCB≌△OCA即可解决问题；

(3)如图3中，连接BN，过点O作OP⊥BD于点P，过点O作OQ⊥AC于点Q，则四边形OPHQ是矩形，可知BN是直径，则HQ=OP=DN=，设AH=x，则AQ=x+，AC=2AQ=2x+9，BC=2x+9，CH=AC﹣AH=2x+9﹣x=x+9，在Rt△AHB中，BH2=AB2﹣AH2=()2﹣x2．在Rt△BCH中，BC2=BH2+CH2即(2x+9)2=()2﹣x2+(x+9)2，解得 x=3，BC=2x+9=15，CH=x+9=12求出sinBCH，即为sin∠ADB的值．

(1)证明：如图1，

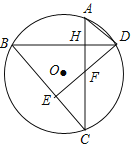
∵AC⊥BD，DE⊥BC，

∴∠AHD=∠BED=90°，

∴∠DAH+∠ADH=90°，∠DBE+∠BDE=90°，

∵∠DAC=∠DBC，

∴∠ADH=∠BDE，

∴BD平分∠ADF；

(2)证明：连接OA、OB．

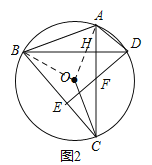
∵OB=OC=OA，AC=BC，

∴△OCB≌△OCA(SSS)，

∴∠OCB=∠OCA，

∴OC平分∠ACB；

(3)如图3中，连接BN，过点O作OP⊥BD于点P，过点O作OQ⊥AC于点Q．

则四边形OPHQ是矩形，

∵DN∥AC，

∴∠BDN=∠BHC=90°，

∴BN是直径，

则OP=DN=，

∴HQ=OP=，

设AH=x，则AQ=x+，AC=2AQ=2x+9，BC=AC=2x+9，

∴CH=AC﹣AH=2x+9﹣x=x+9

在Rt△AHB中，BH2=AB2﹣AH2=()2﹣x2．

在Rt△BCH中，BC2=BH2+CH2，

即(2x+9)2=()2﹣x2+(x+9)2，

整理得2x2+9x﹣45=0，

(x﹣3)(2x+15)=0，

解得： x=3(负值舍去)，

BC=2x+9=15，CH=x+9=12

∵∠ADB=∠BCH，

∴sin∠ADB=sin∠BCH===．

即sin∠ADB的值为．