题目内容
【题目】如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,连接AD.
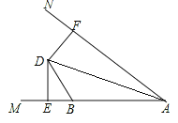
(1)求证:AD平分∠MAN;
(2) 在射线AN上取一点C,使得DC=DB,若AB=6,BE=2,则AC长为____.
【答案】(1)见解析;(2)6或10.
【解析】
(1)根据角平分线的性质即可得到结论;
(2)分两种情况:当点C在线段AF上,Rt△DEB≌Rt△DFC,CF=BE;当点C在线段AF的延长线上时,Rt△DEB≌Rt△DFC,可得到CF=BE.
(1)证明:∵D是∠MAN内部一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,
∴AD平分∠MAN (在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上);
(2)分两种情况:
①如图1,当点C在线段AF上时,
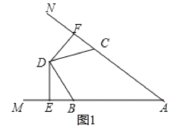
∵DE⊥AM于E,DF⊥AN于F,
∴∠DEB=∠DFC=90°,
在Rt△DEB和Rt△DFC中,
![]() ,
,
∴Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∴AC=AB=6,
②如图2,当点C在线段AF的延长线上时,
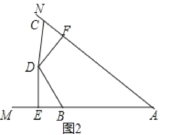
同理可证Rt△DEB≌Rt△DFC,
∴CF=BE=2,
∵AF=AE=AB+BE=8,
∴AC=8+2=10.
故答案为:6或10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目