题目内容
【题目】在平面直角坐标系中,O为坐标原点,点A(8,0)动点P从A出发以每秒2个单位长度的速度沿线段AO向终点O运动,同时动点Q从O出发以相同速度沿y轴正半轴运动,点P到达点O,两点同时停止运动.
(1)当t= 时,∠OPQ=45°;
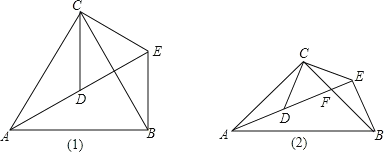
(2)如图2,以PQ为斜边在第一象限作等腰Rt△PQM,求M点坐标;
(3)在(2)的条件下,点R位x轴负半轴上一点,且![]() ,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
【答案】(1)t=2;(2)M(4,4);(3)t为![]() 秒或
秒或![]() 秒时,△ONR为等腰直角三角形.
秒时,△ONR为等腰直角三角形.
【解析】
(1)先由运动知,OP=8-2t,OQ=2t,根据等腰直角三角形的性质即可得结论;
(2)先判断出△MCQ≌△MBP,得出CQ=BP,MC=MB,即可得出点M的纵横坐标相等,用CQ=BP建立方程即可得出结论;
(3)利用等腰直角三角形和对称性确定出点N的坐标,分三种情况讨论计算即可得出结论.
(1)由运动知,AP=2t,OQ=2t,
∵A(8,0),
∴OA=8,
∴0t<4,OP=82t,
在Rt△POQ中,∠OPQ=45°,
∴∠OQP=45°,
∴OP=OQ,
∴82t=2t,
∴t=2
(2)如图2,
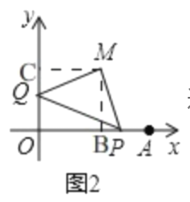
过点M作MB⊥x轴于B,作MC⊥y轴于C,
∴四边形OBMC是矩形,
∴∠BMC=90°,
∵△PMQ是等腰直角三角形,
∴MQ=MP,∠PMQ=90°,
∴∠CMQ=∠BMP,
在△MCQ和△MBP中,
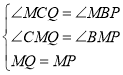 ,
,
∴△MCQ≌△MBP,
∴CQ=BP.MC=MB,
∴设M(m,m),
∴B(m,0),C(0,m),
∵OQ=2t,OP=82t,
∴Q(0,2t),P(82t,0),
∴CQ=|m2t|.BP=|82tm|,
∴|m2t|=|82tm|,
∴m=4,
∴M(4,4),
(3)如图,∵点M,N关于PQ对称,
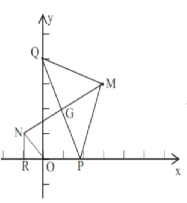
∴点G是MN的中点,MN⊥PQ于G,
∵△PMQ是等腰直角三角形,
∴QG=PG,
∴点G是PQ的中点,
由(2)知,Q(0,2t),P(82t,0),
∴G(4t,t),
∴点N(42t,2t4),
∵点R为x轴负半轴上一点,且OR=![]() OP
OP
∴R(t4,0),
∵△ONR为等腰直角三角形,
∴①、当∠ORN=90°,OR=RN时,
∴点N,R的横坐标相等,
∴4-2t=t4,
∴t=![]() ,
,
②当∠RON=90°,ON=OR时,
∴点N在y轴上,
∴4-2t=0,4-t=2t-4
∴t=2,t=![]() ,此种情况不存在;
,此种情况不存在;
③当∠ONR=90°,ON=NR时,
∴点N在OR的垂直平分线上,且点N到OR的距离等于![]() OR,
OR,
∴4-2t=![]() (t-4+0)①,且|2t-4|=
(t-4+0)①,且|2t-4|=![]() |4-t|②,
|4-t|②,
解①得,t=![]() ,解②得,t=
,解②得,t=![]() 或t=
或t=![]() ,
,
∴t=![]() ,
,
即:t为![]() 秒或
秒或![]() 秒时,△ONR为等腰直角三角形.
秒时,△ONR为等腰直角三角形.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】随着我国网络信息技术的不断发展,在课堂中恰当使用信息技术辅助教学是时代提出的新要求,阳谷县为了解初中数学老师对“网络画板”信息技术的掌握情况,对部分初中数学老师进行了调查,并根据调查结果绘制成如下不完整的统计图表.
掌握情况 | 非常熟练 | 比较熟练 | 不太熟练 | 基本不会 |
人数 | 20 |
| 16 |
|
请根据图表信息,解答下列问题:
(1)求表中![]() 的值;
的值;
(2)求图中表示“比较熟练”的扇形部分的圆心角的度数;
(3)阳谷县共有初中数学教师350人,若将“非常熟练”和“比较熟练”作为“良好”标准,试估计阳谷县初中数学教师对“网络画板”信息技术掌握情况为“良好”的教师有多少人?