题目内容
【题目】如图1,△ACB和△DCE均为等边三角形,点A. D.E在同一直线上,连接BE.
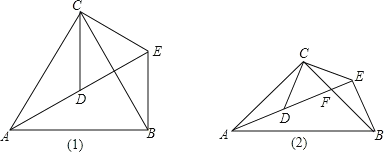
填空:(1),①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 ;
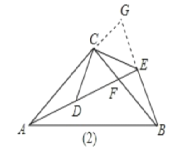
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,且交BC于点F,连接BE.若∠CAF=∠BAF,BE=2,试求AF的长.
【答案】(1)①60°;②AD=BE;(2)4.
【解析】
(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数;
(2)仿照(1)中的解法可求出∠AEB的度数,延长BE交AC的延长线于点G,推出△ACF≌△BCG,根据全等三角形的性质得到AF=BG,由于∠CAF=∠BAF,∠AEB=90°,求得E是BG的中点,即可求出AF=4.
(1)①如图1,
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
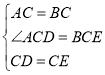 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE;
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
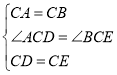 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC∠CED=90°;
延长BE交AC的延长线于点G,
在△ACF和△BCG中,
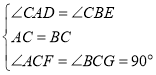 ,
,
∴△ACF≌△BCG,
∴AF=BG,
∵∠CAF=∠BAF,∠AEB=90°,
∴E是BG的中点,
∵BE=2,
∴AF=4.

 精英口算卡系列答案
精英口算卡系列答案