��Ŀ����
����Ŀ��ij��˾�ڹ����б�ʱ���ӵ��ס����������̶ӵ�Ͷ���飮ÿʩ��һ�죬�踶���̶ӹ��̿�1.5��Ԫ�����ҹ��̶ӹ��̿�1.1��Ԫ�������쵼С����ݼס������ӵ�Ͷ������㣬�γ���������ʩ��������
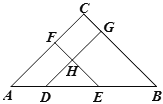
���������ӵ�����ɴ���̸պ������깤��
���������Ҷӵ�����ɴ����Ҫ�ȹ涨���ڶ���5�죻
�����������ס������Ӻ���4�죬ʣ�µĹ������ҶӶ���Ҳ���������깤��
��1����ס������ӵ�����ɴ���̸�������죿
��2��������̲��������깤����˾ÿ�콫��ʧ3000Ԫ��������ǹ�˾�������������һ��ʩ���������㣬��˵�����ɣ�
���𰸡���1���ӵ�����ɴ������20�죬���Ҷӵ�����ɴ������25�죻��2��������ʩ���������ʡ���̿
��������
��1����ӵ�����ɴ������x�죬���Ҷӵ�����ɴ�����裨x+5���죮��ù涨�����ĵ�����ϵΪ�����Һ���4��Ĺ�������+�������涨������4����Ĺ�����=1���ݴ��г����̲����
��2�����ݣ�1���Ľ��ۿ��Եõ�����ʩ���������ֱ����ÿһʩ�������ķ��ã�Ȼ��Ƚϣ�ȡ��������ٵķ�������
��1����ӵ�����ɴ������x�죬���Ҷӵ�����ɴ�����裨x+5���죮
�����⣬�ã�![]() +
+![]() +
+![]() =1��
=1��
��ã�x=20��
�����飺x=20��ԭ��ʽ���̵Ľ⣮
�ࣨx+5��=25��
�𣺼ӵ�����ɴ������20�죬���Ҷӵ�����ɴ������25�죻
��2���ɣ�1���õ����ӵ�����ɴ������20�죬���Ҷӵ�����ɴ������25�죮
������ʩ��������Ҫ�Ĺ��̿�Ϊ��
����1��1.5��20=30����Ԫ����
����2��1.1����20+5��+5��0.3=29����Ԫ����
����3��1.5��4+1.1��20=28����Ԫ����
��30��29��28��
��������ʩ���������ʡ���̿

����Ŀ��ѧУ���ʹ�����һ������120�ִ���֧Ԯɽ�������мס��ҡ������ֳ���ѡ��ÿ�����������������˷����±���ʾ(����ÿ����������)��
���� | �� | �� | �� |
����������(��/��) | 5 | 8 | 10 |
�����˷�(Ԫ/��) | 400 | 500 | 600 |
(1)��ȫ�����ʶ��üס������ֳ������ͣ����˷�8200Ԫ����ֱ���ס������ֳ���������
(2)Ϊ�˽�ʡ�˷ѣ��ù�˾�����üס��ҡ������ֳ�ͬʱ�������ͣ���֪���ǵ�������Ϊ14��������ֱ�������ֳ����������������ʱ���˷ѣ�