Question

【题目】某商场销售一种商品的进价为每件30元，销售过程中发现月销售量y（件）与销售单价x（元）之间的关系如图所示．

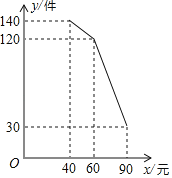
（1）根据图象直接写出y与x之间的函数关系式．

（2）设这种商品月利润为W（元），求W与x之间的函数关系式．

（3）这种商品的销售单价定为多少元时，月利润最大？最大月利润是多少？

Answer 1

【答案】（1）y＝；（2）W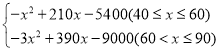＝;（3）这种商品的销售单价定为65元时，月利润最大，最大月利润是3675．

【解析】

（1）当40≤x≤60时，设y与x之间的函数关系式为y=kx+b，当60＜x≤90时，设y与x之间的函数关系式为y=mx+n，解方程组即可得到结论；

（2）当40≤x≤60时，当60＜x≤90时，根据题意即可得到函数解析式；

（3）当40≤x≤60时，W=-x2+210x-5400，得到当x=60时，W最大=-602+210×60-5400=3600，当60＜x≤90时，W=-3x2+390x-9000，得到当x=65时，W最大=-3×652+390×65-9000=3675，于是得到结论．

解：（1）当40≤x≤60时，设y与x之间的函数关系式为y＝kx+b，

将（40，140），（60，120）代入得，

解得：，

∴y与x之间的函数关系式为y＝﹣x+180；

当60＜x≤90时，设y与x之间的函数关系式为y＝mx+n，

将（90，30），（60，120）代入得，

解得：，

∴y＝﹣3x+300；

综上所述，y＝；

（2）当40≤x≤60时，W＝（x﹣30）y＝（x﹣30）（﹣x+180）＝﹣x2+210x﹣5400，

当60＜x≤90时，W＝（x﹣30）（﹣3x+300）＝﹣3x2+390x﹣9000，

综上所述，W＝；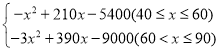

（3）当40≤x≤60时，W＝﹣x2+210x﹣5400，

∵﹣1＜0，对称轴x＝＝105，

∴当40≤x≤60时，W随x的增大而增大，

∴当x＝60时，W最大＝﹣602+210×60﹣5400＝3600，

当60＜x≤90时，W＝﹣3x2+390x﹣9000，

∵﹣3＜0，对称轴x＝＝65，

∵60＜x≤90，

∴当x＝65时，W最大＝﹣3×652+390×65﹣9000＝3675，

∵3675＞3600，

∴当x＝65时，W最大＝3675，

答：这种商品的销售单价定为65元时，月利润最大，最大月利润是3675．