��Ŀ����
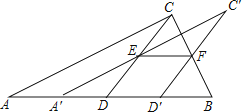
����Ŀ����ͼ���ڳ�����ABCD�У�AB=4cm��BC=6cm����EΪAB�е㣬�����P���߶�BC����ÿ��2cm���ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CD���ɵ�C���D�˶������˶�ʱ��Ϊt��.
(1)��t=2ʱ�����EBP�����
(2)����Q�����P��ͬ���ٶ��˶�������������BPE����CQPȫ�ȣ���ʱ��Q���ٶ��Ƕ��٣�
(3)����Q��(2)�е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ���س�����ABCD���ı��˶������ʱ���P���Q��һ���ڳ�����ABCD����������������

���𰸡���1��4cm2����2������1.5���BPE���CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s��3������9���P���Q��һ����AB��������.
cm/s��3������9���P���Q��һ����AB��������.
��������
��EBP���������![]() EB��BP��ã���t��EP BP��ʾ������;
EB��BP��ã���t��EP BP��ʾ������;
��2����� Q ���˶��ٶ�Ϊx cm/s���ȸ���ʱ�䡢�ٶȱ�ʾ·��: BP=2t��CP=6-2t��![]() �����ݵ�EΪAB�е��ʾEB=2��������BPE����CPQȫ�ȣ�������������ֱ���ݶ�Ӧ����ȣ��з��̿ɵý��ۣ�
�����ݵ�EΪAB�е��ʾEB=2��������BPE����CPQȫ�ȣ�������������ֱ���ݶ�Ӧ����ȣ��з��̿ɵý��ۣ�
��3����t��ʾ����P�͵�Q��·�̣�������ȣ����t��ֵ���ٸ��������ж��Ƿ�Ϊ��һ������.
�⣺��1����t=2
��BP=2t=4
��E��AB���е㣬AB=4
��EB=2
��S��EBP=![]() EB��BP=4cm2
EB��BP=4cm2
��2����� Q ���˶��ٶ�Ϊx cm/s���� BP=2t��CP=6-2t��![]()
�ߡ�B=��C=90��
�ٵ�BP=CP��BE=CQʱ����BPE�ա�CPQ
��![]()
��ã�
�ڵ�BP=CQ��BE=CPʱ����BPE�ա�CQP
��![]()
��ã�![]()
��x��2
����ȥ�������
��������������1.5����BPE����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s
cm/s
��3��������ã�2t=![]() t+6
t+6
��ã�t=9
��t=9ʱ����P����2��9=18cm
�� 18-BC-CD-AD=2
�� ����9���P���Q��һ����AB��������