Question

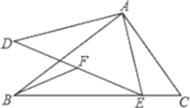
【题目】如图，△ABC∽△ADE，∠BAC＝∠DAE＝90°，AB＝16，AC＝12，F是DE的中点， 若点E是直线BC上的动点，连接BF，则BF的最小值是____．

Answer 1

【答案】8

【解析】

根据相似三角形的性质得到∠ADE=∠ABE，推出点A，D，B，E四点共圆，得到∠DBE=90°，根据直角三角形的性质得到，当DE最小时，BF的值最小，DE最小，根据相似三角形的性质即可得到结论．

解：如图，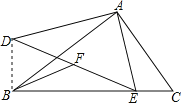

∵△ABC∽△ADE，
∴∠ADE=∠ABE，
∴点A，D，B，E四点共圆，
∵∠DAE=90°，
∴∠DBE=90°，
∵F是DE的中点，

，

∴当DE最小时，BF的值最小，
∵若点E是直线BC上的动点，
∴当AE⊥BC时，AE最小，此时，DE最小，
∵∠BAC=90°，AB=16，AC=12，
∴BC=20，

，

∵△ABC∽△ADE，

，

，

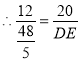∴DE=16，
∴BF=8，
故答案为：8．