题目内容
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造□PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.

(1)求证:四边形ADEC是平行四边形;
(2)以线段PE为对角线作正方形MPNE,点M、N分别在第一、四象限.
①当点M、N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M、N中恰好只有一点落在四边形ADEC的内部(不包括边界)时,设□PCOD的面积为S,直接写出S的取值范围.
【答案】(1)证明见解析;(2)t=![]() 或t=1;(3)
或t=1;(3)![]() ≤S<2.
≤S<2.
【解析】
试题分析:(1)连接CD交OP于点G,由PCOD的对角线互相平分,得四边形ADEC是平行四边形;
(2)①第一种情况,当点M在CE边上时,由△EMF∽△ECO,再利用正方形对角线相等求解;第二种情况,当点N在DE边上时,由△EFN∽△EPD,再利用正方形对角线相等求解;
②当![]() ≤t≤1时,求出S的取值范围.
≤t≤1时,求出S的取值范围.
试题解析:(1)如图1,连接CD交AE于F,
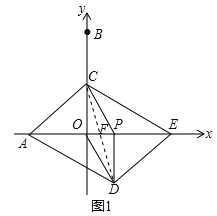
∵四边形PCOD是平行四边形,
∴CF=DP,OF=PF,
∵PE=AO,
∴AF=EF,又CF=DP,
∴四边形ADEC为平行四边形;
(2)①当M点在CE上时,第一种情况:如图,当点M在CE边上时,

∵MF∥OC,
∴△EMF∽△ECO,
∴![]() ,
,
∵四边形MPNE为正方形,
∴MF=EF,
∴CO=EO,即4-2t=t+2,
∴t=![]() ;
;
第二种情况:当点N在DE边时,
∵NF∥PD,
∴△EFN∽△EPD,
∴![]() ,
,
∵四边形MPNE为正方形,
∴NF=EF,
∴PD=PE,即4-2t=2,
∴t=1;
∴当点M、N中有一点落在四边形ADEC的边上时,所有满足条件的t的值为t=![]() 或t=1;
或t=1;
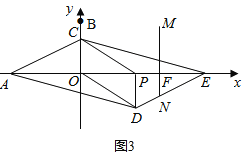
②∵![]() ≤t≤1,
≤t≤1,
S=(4-2t)t=-2t2+4t=-2(t-1)2+2,
∴点M、N中恰好只有一点落在四边形ADEC的内部(不包括边界)时,![]() ≤S<2.
≤S<2.

 阅读快车系列答案
阅读快车系列答案