��Ŀ����
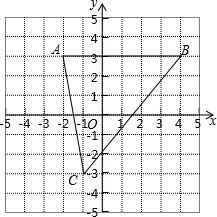
����Ŀ����ͼ��1����AB=7cm��AC��AB��BD��AB ����ֱ�Ϊ A��B��AC=5cm����P ���߶� AB ���� 2cm/s ���ٶ��ɵ� A ���B �˶���ͬʱ���� Q ������ BD ���˶��������� ����ʱ��Ϊ t��s�������� P �˶�����ʱ���� Q �˶���֮��������
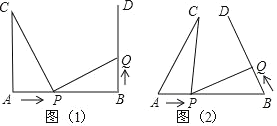
��1������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ��� t=1 ʱ����ACP ����BPQ �Ƿ�ȫ�ȣ� ���жϴ�ʱ�߶� PC ���߶� PQ ��λ�ù�ϵ����ֱ�˵�����ɣ�
��2����ͼ��2��������AC��AB��BD��AB�� ��Ϊ ����CAB=��DBA=60�㡱���� Q ���˶��� ��Ϊ x cm/s�������������䣬���� P��Q �˶���ij��ʱ������ACP ����BPQ ȫ�ȣ������Ӧ�� x��t ��ֵ��
���𰸡���1����ACP�ա�BPQ��PC��PQ�����ɼ���������2��t=1s��x=2cm/s��t=![]() s��x=
s��x=![]() cm/s��
cm/s��
��������
��1������SAS֤�á�ACP�ա�BPQ���ó���ACP=��BPQ�����ɵó���APC+��BPQ=��APC+��ACP=90�������ɵó����ۣ�
��2���ɡ�ACP�ա�BPQ���������������AC=BP��AP=BQ����AC=BQ��AP=BP��������������ô𰸼��ɣ�
�⣺��1����ACP�ա�BPQ��PC��PQ��
�������£���t=1ʱ��AP=BQ=2��
��BP=7-2=5��
��BP=AC��
��AC��AB��BD��AB
���A=��B=90��
�ڡ�ACP�͡�BPQ�У�
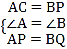 ��
��
���ACP�ա�BPQ��
���ACP=��BPQ��
���APC+��BPQ=��APC+��ACP=90����
���CPQ=90����
��PC��PQ��
��2��������ACP�ա�BPQ��
��AC=BP��AP=BQ���ɵã�5=7-2t��2t=xt
��ã�x=2��t=1��
������ACP�ա�BQP��
��AC=BQ��AP=BP���ɵã�5=xt��2t=7-2t
��ã�t=![]() �� x=5��
�� x=5��![]() =
=![]() ��
��
�ʵ�t=1s��x=2cm/s��t=![]() s��x=
s��x=![]() cm/sʱ����ACP���BPQȫ�ȣ�
cm/sʱ����ACP���BPQȫ�ȣ�