Question

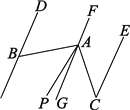
【题目】已知如图，直线AB、CD相交于O，OE平分∠BOD，OF平分∠COB，∠2∶∠1=4∶1，求∠AOF的度数.

解：∵OE平分∠BOD　

∴∠BOD=＿＿∠1　

∵=4　

∴∠2=＿＿∠1　

∵∠2＋∠BOD=＿＿＿＿　

∴4∠1+2∠1=

∴∠1=30°

∴∠BOD = ；

∴∠AOC= ；

又∵∠BOD+∠BOC=180°

∴∠BOC=120°

∵ OF平分∠COB

∴∠COF=∠BOF= ；

∴∠AOF=60°+60°= .

Answer 1

【答案】答案见解析

【解析】试题分析：由OE平分∠BOD可得出∠BOD=2∠1，由=4，可得∠2=4∠1，又因为∠2＋∠BOD=180°得出4∠1+2∠1=180°，解得∠1=30°，所以∠BOD =∠AOC=60°，

进而求出∠BOC=120°，再根据OF平分∠COB可求得∠COF=∠BOF=60，最后计算出∠AOF的度数即可.

试题解析：

解：如图∵OE平分∠BOD，　

∴∠BOD=2∠1，　

∵=4，　

∴∠2=4∠1，　

∵∠2＋∠BOD=180°，　

∴4∠1+2∠1=180°，

∴∠1=30°，

∴∠BOD =60°；

∴∠AOC=60°；

又∵∠BOD+∠BOC=180°，

∴∠BOC=120°，

∵OF平分∠COB，

∴∠COF=∠BOF=60°，

∴∠AOF=60°+60°=120°.