题目内容
【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证: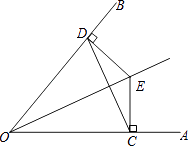
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线.
【答案】
(1)
解:∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB,
∴EC=ED,
∴∠ECD=∠EDC;
(2)
解:在Rt△ODE和Rt△OCE中,
∵ ![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OC=OD,
又∵DE=CE,
∴OE是CD的垂直平分线.
【解析】(1)由角平分线的性质即可得证;(2)根据“HL”证Rt△ODE≌Rt△OCE,得OC=OD,由DE=CE可得OE是CD的垂直平分线.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
相关题目