题目内容
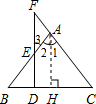 (1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.
(1)如图,在△ABC中,AB=AC,D是底边BC上的一点,过点D作BC的垂线,交AB于点E,交AC的延长线于F,则△AEF是等腰三角形.请在解答过程中的括号里填写理由.解:作AH⊥BC于H
∵AB=AC(已知)
∴∠1=∠2
(等腰三角形三线合一)
(等腰三角形三线合一)
∵DF⊥BC(已知)
∴AH∥DF(平面内垂直于同一条直线的两直线平行)
∴∠1=∠F
(两直线平行,同位角相等)
(两直线平行,同位角相等)
∠2=∠3
(两直线平行,内错角相等)
(两直线平行,内错角相等)
∴∠F=∠3(等量代换)
∴AE=AF
(等角对等边)
(等角对等边)
∴△AEF是等腰三角形.
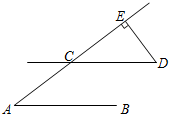
(2)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=36°,求∠D的度数.
分析:(1)根据等腰三角形三线合一的性质,及平行线的性质以及等角对等边的性质分别填空即可;
(2)先根据两直线平行,同位角相等求出∠DCE=∠A,再根据三角形的内角和定理列式进行计算即可求解.
(2)先根据两直线平行,同位角相等求出∠DCE=∠A,再根据三角形的内角和定理列式进行计算即可求解.
解答:解:(1)等腰三角形三线合一;
两直线平行,同位角相等;
两直线平行,内错角相等;
等角对等边;
(2)∵AB∥CD,∠A=36°,
∴∠DCE=∠A=36°,
∵DE⊥AE,
∴∠D=180°-90°-36°=54°.
故答案为:54°.
两直线平行,同位角相等;
两直线平行,内错角相等;
等角对等边;
(2)∵AB∥CD,∠A=36°,
∴∠DCE=∠A=36°,
∵DE⊥AE,
∴∠D=180°-90°-36°=54°.
故答案为:54°.
点评:本题主要考查了等腰三角形的性质,平行线的性质,题目比较简单,熟练掌握性质是解题的关键.

练习册系列答案
相关题目
 16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( ) 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, 16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( )
16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( ) 18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数.
18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数. 如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )
如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )