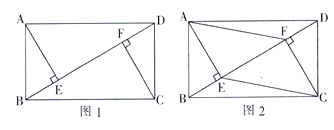
题目内容
【题目】已知四边形![]() 是正方形,
是正方形,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
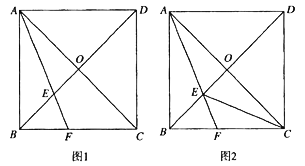
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
【答案】(1)见解析;(2)![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
【解析】
(1)取AF的中点G,连接OG,根据三角形的中位线得出OG=![]() FC,OG//FC,根据正方形的性质求出∠0AB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
FC,OG//FC,根据正方形的性质求出∠0AB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
(2)由已知条件和三角形内角和定理可得∠DAE=∠DEA,∠DEC=∠DCE,∠BEF=∠BFE,进而可得△DAE;△DCE;△BEF是等腰三角形,由垂直平分线的性质可得AE=CE进而可得△AEC是等腰三角形.
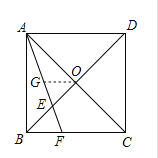
解:证明:(1)如图:取![]() 的中点G,连接OG.
的中点G,连接OG.
∵正方形![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)
∵四边形ABCD是正方形,
∴BD⊥AC,AO=CO,∠BAC=∠DAC=45°,
∴AE=CE,
∴△AEC是等腰三角形;
∵过点A作∠BAC的平分线分别交BD、BC于E、F,
∴∠BAF=∠CAF=22.5°,
∴∠DAE=67.5°,
∴∠AED=67.5°,
∴AD=ED,
∴△ADE是等腰三角形,AE=CE,
∵∠ECA=∠EAC=22.5°,
∴∠ECD=67.5°,
∴∠DEC=∠DCE=67.5°,
∴DE=CE,
∴△DEC是等腰三角形,
∵∠BEF=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形.
可直接写出图中所有的等腰三角形有:![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.若不够卡购物和使用优惠卡购物分别视为方式一购物和方式二购物,且设顾客购买商品的金额为![]() 元.
元.
(Ⅰ)根据题意,填写下表:
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … | |
方式二的总费用(元) | 540 | … |
(Ⅱ)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?
(Ⅲ)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(Ⅳ)小张按合算的方案,把这台冰箱买下,如果该商场还能盈利![]() ,那么这台冰箱的进价是多少元?
,那么这台冰箱的进价是多少元?