题目内容
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
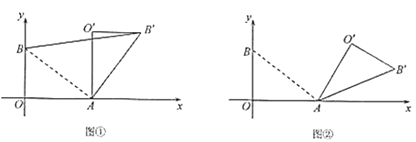
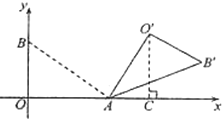
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(Ⅲ)记![]() 为
为![]() 的中点,S为
的中点,S为![]() 的面积,求S的取值范围(直接写出结果即可).
的面积,求S的取值范围(直接写出结果即可).
【答案】(Ⅰ)![]() ;(Ⅱ)点
;(Ⅱ)点![]() 的坐标为
的坐标为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)利用勾股定理求出AB的长,根据旋转的性质可得∠BAB′=90°,AB=AB′,利用勾股定理求出BB′的长即可;(Ⅱ) 点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,由旋转的性质可得
,由旋转的性质可得![]() ,
,![]() .即可求出∠O′AC=60°,利用∠O′AC的三角函数可求出OC和AC的长,进而可得OC的长,即可得答案;(Ⅲ)由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,可得O′在AB上时S最小,O′在BA的延长线上时S最大,先求出KO′的长,进而求出S的值即可得答案.
.即可求出∠O′AC=60°,利用∠O′AC的三角函数可求出OC和AC的长,进而可得OC的长,即可得答案;(Ⅲ)由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,可得O′在AB上时S最小,O′在BA的延长线上时S最大,先求出KO′的长,进而求出S的值即可得答案.
(Ⅰ)∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
根据题意,![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,
得到的,
由旋转的性质,可得![]() ,
,![]() .
.
∴在![]() 中,
中,![]() .
.
(Ⅱ)如图,根据题意,由旋转的性质,
可得![]() ,
,![]() .
.
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则
,则![]() .
.
在![]() 中,
中,
由![]() ,
,
得![]() ,
,
![]() .
.
有![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
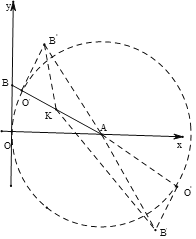
(Ⅲ)如图,由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,
∴O′在AB上时S最小,O′在BA的延长线上时S最大,
当O′在AB上时,
∵K为AB中点,
∴AK=![]() ,
,
∴KO′=4-![]() =
=![]()
∴S=![]() ×
×![]() ×3=
×3=![]() ,
,
当O′在BA的延长线上时,KO′=AK+AO′=![]() +4=
+4=![]() ,
,
∴S=![]() ×
×![]() ×3=
×3=![]() ,
,
∴S的取值范围为:![]() ≤S≤
≤S≤![]() .
.

【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本,每本价格为2元.在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为![]() 元,在乙文具店购买这种笔记本的付款金额为
元,在乙文具店购买这种笔记本的付款金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)当![]() 时,在哪家文具店购买这种笔记本的花费少?请说明理由.
时,在哪家文具店购买这种笔记本的花费少?请说明理由.
【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.