题目内容
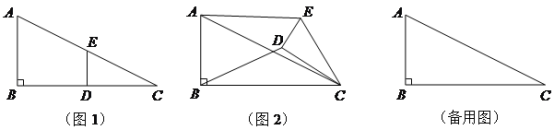
【题目】如图，已知∠BAC=∠ADE=90°，AD⊥BC，AC=DC.关于优弧CAD，下列结论正确的是（ ）
A.经过点B和点EB.经过点B，不一定经过点E
C.经过点E，不一定经过点BD.不一定经过点B和点E
【答案】B
【解析】
由条件可知BC垂直平分AD，可证△ABC≌△DBC，可得∠BAC=∠BDC=90°故∠BAC+∠BDC=180°则A、B、D、C四点共圆，即可得结论.
解：如图：设AD、BC交于M
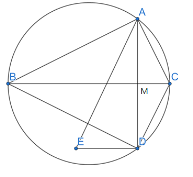
∵AC=CD，AD⊥BC
∴M为AD中点
∴BC垂直平分AD
∴AB=DB
∵BC=BC，AC=CD
∴△ABC≌△DBC
∴∠BAC=∠BDC=90°
∴∠BAC+∠BDC=180°
∴A、B、D、C四点共圆
∴优弧CAD经过B，但不一定经过E
故选 B
练习册系列答案
名校课堂系列答案
相关题目
