题目内容
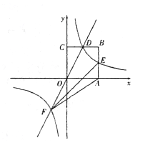
【题目】已知抛物线![]() ,直线
,直线![]() ,直线
,直线![]()
(1)当m=0时,若直线![]() 经过此抛物线的顶点,求b的值
经过此抛物线的顶点,求b的值
(2)将此抛物线夹在![]() 之间的部分(含交点)图象记为
之间的部分(含交点)图象记为![]() ,若
,若![]() ,
,
①判断此抛物线的顶点是否在图象![]() 上,并说明理由;
上,并说明理由;
②图象![]() 上是否存在这样的两点:
上是否存在这样的两点:![]() ,其中
,其中![]() ?若存在,求相应的
?若存在,求相应的![]() 和
和![]() 的取值范围
的取值范围
【答案】(1)b=-2;(2)①不在,理由详见解析;②不存在,理由详见解析.
【解析】
(1) 把m=0代入即可求出抛物线解析式,则可得顶点坐标为,把顶点坐标代入![]() ,可求得b的值;
,可求得b的值;
(2)①将抛物线化成顶点式![]() 后,得出抛物线顶点为(m,2m-2).当x=m时,对于
后,得出抛物线顶点为(m,2m-2).当x=m时,对于![]() ,对于
,对于![]() 由于
由于![]() ,可得
,可得![]() 顶点(m,2m-2)在
顶点(m,2m-2)在![]() 的下方,即可得出结论;②设直线
的下方,即可得出结论;②设直线![]() 与抛物线交于A、B两点,且
与抛物线交于A、B两点,且![]() ,由方程
,由方程![]() ,可得
,可得![]() ,此时
,此时![]() ;设直线
;设直线![]() 与抛物线交于C,D两点,且
与抛物线交于C,D两点,且![]() ,由方程
,由方程![]() ,可得
,可得![]() ,此时
,此时![]() 可得
可得![]() ,可判断
,可判断![]() 由于
由于![]() ,即点A在抛物线对称轴的左侧,则在抛物线对称轴的右侧,必存在点A的对称点
,即点A在抛物线对称轴的左侧,则在抛物线对称轴的右侧,必存在点A的对称点![]() ,其中
,其中![]() , 所以
, 所以![]() ,由于抛物线的开口向上,可得当x<m时,y随x的增大而减小,由于抛物线顶点在
,由于抛物线的开口向上,可得当x<m时,y随x的增大而减小,由于抛物线顶点在![]() 的下方,故点C也在抛物线对称轴左侧,设
的下方,故点C也在抛物线对称轴左侧,设![]() 是抛物线上A、C两点之间的任意一点,则有
是抛物线上A、C两点之间的任意一点,则有![]() ,故
,故![]() ,又因为在抛物线上必存在其对称点
,又因为在抛物线上必存在其对称点 ![]() ,其中
,其中![]() ,故
,故![]() ,故抛物线上A、C两点之间的任意点的对称点都在点D下方.同理,抛物线上B、D两点之间的部分所有点的对称点都在点A上方,所以图像C上不存在这样的两点:
,故抛物线上A、C两点之间的任意点的对称点都在点D下方.同理,抛物线上B、D两点之间的部分所有点的对称点都在点A上方,所以图像C上不存在这样的两点:![]() 和
和![]() ,其中
,其中![]()
(1)解:当m=0时,抛物线:![]()
则顶点坐标为(0,-2)
把(0,-2)代入![]() ,可得b=-2
,可得b=-2
(2)①抛物线的顶点不在图像C上,理由如下:
因为![]() ,
,
所以抛物线顶点为(m,2m-2)
当x=m时,对于![]() ,对于
,对于![]()
因为![]()
所以![]()
所以![]()
即顶点在![]() 的下方
的下方
所以抛物线的顶点不在图像C上
②解:设直线![]() 与抛物线交于A、B两点,且
与抛物线交于A、B两点,且![]()
![]()
解得![]()
因为![]() ,且对于
,且对于![]() ,y随x的增大而增大
,y随x的增大而增大
所以![]()
所以![]() ,此时
,此时![]()
设直线![]() 与抛物线交于C,D两点,且
与抛物线交于C,D两点,且![]()
![]()
所以![]()
所以![]()
因为![]()
所以![]() ,
,
所以 ![]()
因为![]() ,且对于
,且对于![]() ,y随x的增大而增大,
,y随x的增大而增大,
所以![]()
所以![]() ,此时
,此时![]()
因为![]() ,
,
又因为![]()
所以![]()
又因为![]()
所以![]() ,即
,即![]()
因为![]() ,即点A在抛物线对称轴的左侧,则在抛物线对称轴的右侧,必存在点A的对称点
,即点A在抛物线对称轴的左侧,则在抛物线对称轴的右侧,必存在点A的对称点![]() ,其中
,其中![]()
所以![]()
因为抛物线的开口向上,
所以当x<m时,y随x的增大而减小,
因为抛物线顶点在![]() 的下方,故点C也在抛物线对称轴左侧,
的下方,故点C也在抛物线对称轴左侧,
设![]() 是抛物线上A、C两点之间的任意一点,则有
是抛物线上A、C两点之间的任意一点,则有![]()
所以![]()
又因为在抛物线上必存在其对称点 ![]() ,其中
,其中![]()
所以![]()
也即抛物线上A、C两点之间的任意点的对称点都在点D下方
同理,抛物线上B、D两点之间的部分所有点的对称点都在点A上方
所以图像C上不存在这样的两点:![]() 和
和![]() ,其中
,其中![]()

 阅读快车系列答案
阅读快车系列答案【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
|
| 0 | 1 | 2 | 3 | 4 |
|
|
| 3 | 0 | -1 | 0 |
|
|
(1)请写出该二次函数图像的开口方向、对称轴、顶点坐标和![]() 的值;
的值;
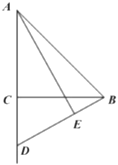
(2)设该二次函数图像与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图像上点
,该图像上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

【题目】为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
小华 | 8 | ||
小亮 | 8 | 3 |
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差 .(填“变大”、“变小”、“不变”)