Question

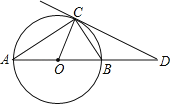
【题目】已知：如图AB为⊙O直径，C是⊙O上一点，D在AB的延长线上，∠DCB＝∠A．

（1）求证：CD是⊙O的切线．

（2）若CD与⊙O相切，且∠D＝30°，BD＝10，求⊙O的半径．

Answer 1

【答案】（1）见解析;（2）10.

【解析】

（1）相切，由已知可证得∠OCD=90°即CD是⊙O的切线；
（2）由已知可推出∠A=∠BCD=30°，即BC=BD=10，从而得到AB=20即可得到半径的长．

（1）CD与⊙O相切．

证明：∵AB为⊙O的直径，C是⊙O上一点，

∴∠ACB＝90°，即∠ACO+∠OCB＝90°；

∵∠A＝∠OCA，且∠DCB＝∠A，

∴∠OCA＝∠DCB，

∴∠OCD＝90°，

∴CD是⊙O的切线．

（2）在Rt△OCD中，∠D＝30°；

∴∠COD＝60°，

∴∠A＝30°，

∴∠BCD＝30°，

∴BC＝BD＝10，

∴AB＝20，

∴⊙O的半径为10．