Question

如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，D、E分别是边AB、AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR‖BA交AC于R，当点Q与点C重合时，点P停止运动．
【小题1】求点D到BC的距离DH的长；
【小题2】设BQ＝x, QR＝y．
① 求y关于x的函数关系式（0≤x≤10）；
② 是否存在点P，使△PQR为等腰三角形？若存在，求出所有满足要求的x的值；若不存在，请说明理由．

Answer 1

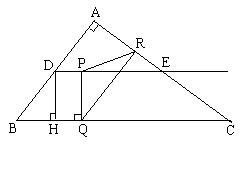
【小题1】在Rt△ABC中，∵AB＝6，AC＝8，∴BC＝10. 　　
∵BC边上的高为，D为AB中点，　　　　　　　
　　　　　
【小题1】①∵QR∥AB，△RQC∽△ABC， .　　　　
　　　　∵BQ＝x，CQ＝10－x,                 
∴,.　　
    　　　（i）当QR为底边时，QM＝y＝，PQ＝DH＝，
作PM⊥QR于M，则△PQM∽△BCA，，
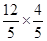＝.解得x₁＝BQ ＝.
（ii）当PR为底边时，QR＝PQ＝，
∵QR∥AB， ，BQ×6＝×10，解得CQ＝4.
∴　x₂＝BQ＝6.
（iii）当PQ为底边时，点R在PQ的垂直平分线上，点R是CE中点.
∵ QR∥AB，∴ ，解得x₃＝BQ＝.
综上所述，当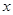为或6或时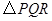，为等腰三角形．解析:

【小题1】根据三角形相似的判定定理求出△BHD∽△BAC，根据相似三角形的性质求出DH的长；
【小题1】①根据△RQC∽△ABC，根据三角形的相似比求出y关于x的函数关系式；
②画出图形，根据图形进行讨论：
① 当PQ=PR时，过点P作PM⊥QR于M，则QM=RM．由于∠1+∠2=90°，∠C+∠2=90°，∴∠1=∠C．
② ∴cos∠1=cosC==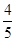，∴，即可求出x的值；
③ 当PQ=RQ时，-x+6=，x=6；
④ 当PR=QR时，则R为PQ中垂线上的点，于是点R为EC的中点，故CR=CE=AC=2．