题目内容
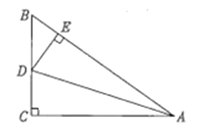
【题目】如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中结论正确的个数有()
=AB:AC.其中结论正确的个数有()
A.5个B.4个
C.3个D.2个
【答案】A
【解析】
由在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E.可得CD=DE,继而可得∠ADC=∠ADE,又由角平分线的性质,证得AE=AD,由等角的余角相等,可证得∠BDE=∠BAC,由三角形的面积公式,可证得S△ABD:S△ACD=AB:AC.
解:∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED,
故①正确;
∴∠CDE=90°∠BAD,∠ADC=90°∠CAD,
∴∠ADE=∠ADC,
即AD平分∠CDE,
故④正确;
∴AE=AC,
∴AB=AE+BE=AC+BE,
故②正确;
∵∠BDE+∠B=90°,∠B+∠BAC=90°,
∴∠BDE=∠BAC,
故③正确;
∵S△ABD=![]() ABDE,S△ACD=
ABDE,S△ACD=![]() ACCD,
ACCD,
∵CD=ED,
∴S△ABD:S△ACD=AB:AC,
故⑤正确.
综上所述,结论正确的是①②③④⑤共5个
故答案为:A.

【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:
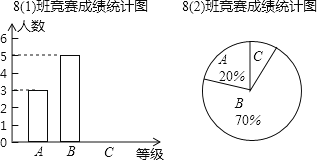
(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;