题目内容
【题目】下面的网格中,每个小正方形的边长均为1个单位.小正方形的顶点叫做格点,以О点为原点,以过О点的水平直线MN为x轴建立平面直角坐标系.
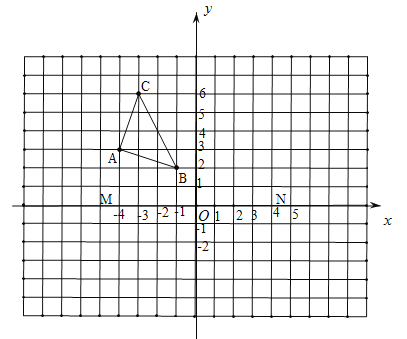
(1)![]() 与格点
与格点![]() 是关于y轴对称,画出
是关于y轴对称,画出![]() ;
;
(2)格点Р在第二象限内,且![]() 为等腰直角
为等腰直角![]() (注:P不在
(注:P不在![]() 的边上),画出
的边上),画出![]() ,并直接写出Р点坐标.
,并直接写出Р点坐标.
【答案】(1)见解析;(2) 图形见解析,![]()
【解析】
(1)利用关于y轴对称点的性质得出对应点位置进而得出答案;
(2)易证△CAB是等腰直角三角形,且∠CAB=90°.然后分三种情况讨论即可得出结论.
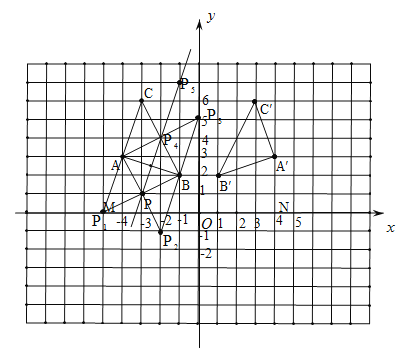
(1)如图所示:![]() ,即为所求;
,即为所求;
(2)∵AC=![]() ,AB=
,AB=![]() ,AC=
,AC=![]() ,
,
AC2+AB2=![]() =10+10=20=BC2,
=10+10=20=BC2,
∴△CAB是等腰直角三角形,且∠CAB=90°.
分三种情况讨论:
①作C关于点A的对称点P1,则△BAP1是等腰直角三角形.设P1(x,y).
∵A(-4,3),C(-3,6),
∴-3+x=2×(-4),6+y=2×3,
解得:x=-3,y=0,
∴P1(-3,0),点P1在x轴上,不符合题意,舍去.
②以B为旋转中心,把BA绕B点逆时针旋转90°得到P2,把BA绕B点顺时针旋转90°得到P3,易得P2(-2,-1)在第三象限,P3(0,5)在y轴上,都不符合题意,舍去;
③作AB的垂直平分线.在第二象限内AB的垂直平分线上有三个格点P、P4、P5.
∵P4在BC上,∴P4不合题意.
∵△ABP5不是直角三角形,∴P5不合题意.
∵AP=![]() ,BP=
,BP=![]() ,AB=
,AB=![]() ,
,
∴AP=BP,AP2+BP2=![]() =5+5=10=AB2,
=5+5=10=AB2,
∴∠APB=90°,∴△APB是等腰直角三角形,∴点P满足条件.
由图可知:点P的坐标为P(-3,1).

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目






