题目内容
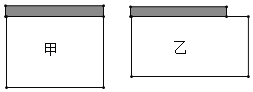
【题目】用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
【答案】当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
【解析】
根据矩形的面积公式甲图列出算式可以直接求面积,乙图设垂直于墙的一边为x,则另一边为(18﹣x)(包括墙长)列出二次函数解析式即可求解.
解:如图甲:设矩形的面积为S,
则S=8×![]() (28﹣8)=80.
(28﹣8)=80.
所以当菜园的长、宽分别为10m、8m时,面积为80;
如图乙:设垂直于墙的一边长为xm,则另一边为![]() (28﹣2x﹣8)+8=(18﹣x)m.
(28﹣2x﹣8)+8=(18﹣x)m.
所以S=x(18﹣x)=﹣x2+18x=﹣(x﹣9)2+81
因为﹣1<0,
当x=9时,S有最大值为81,
所以当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
综上:当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目