题目内容
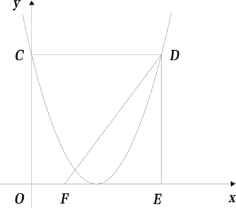
【题目】已知二次函数
的图象与
轴交于点C，过点C作CD∥
轴交该函数的图象于点D，过点D作DE∥轴交轴于点E，已知点F（1，0），连接DF.
（1）请求出该函数图象的项点坐标（用含
的代数式表示）；
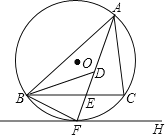
（2）如图，若该二次函数的图象的顶点落在轴上，P为对称轴右侧抛物线上一点；
①连接PD、PE、PF，若
，求点P的坐标；
②若∠PFD=
∠DEF，点P的横坐标为m，则m的值为 .
【答案】（1）顶点坐标（2，
）；（2）①P（
，
）；②
【解析】
（1）根据顶点坐标公式，代入计算即可；
（2）该二次函数的图象的顶点落在
轴上，可求得a的值，即可得函数解析式①由FD坐标可求得直线FD的解析式，设
可得Q点坐标，分别表达出
以及
，列出方程计算即可得出m的值；②连接CE，交FD于N,延长FP交CE于M,由条件可得△CND∽△FNM故
，联立
及FD解析式可求得
，由长度公式可算出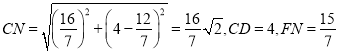
可求得
，设M（t，-t+4），列出方程
求出
可得直线FM的函数解析式：
，联立抛物线解析式即可求出交点的横坐标m.
（1）∵
∴
∴
∴顶点坐标为（2，4-4a）
（2）∵该二次函数的图象的顶点落在轴上
∴4-4a=0
∴a=1
∴
①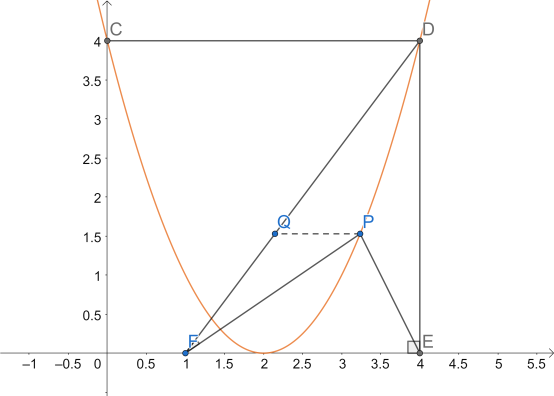
设直线FD的解析式为
把F(1,0) D(4,4)代入可得：
∴
∴
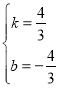
∴设
当
时
∴
∴
∴
∴
∵
∴
∴
当m=4，P（4，4）时，P、D重合，不存在△PDE以及△PDF
∴
∴
② 连接CE，交FD于N,延长FP交CE于M
∵∠PFD=
∠DEF
∴∠DCE=∠NFP=45°
∵∠DNC=∠MNF
∴△CND∽△FNM
∴
∵C（0，4），E（4，0）
∴
∵
∴
∴
∴
∴
∴
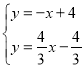
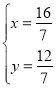
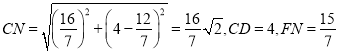
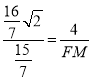
设M（t，-t+4）
∴
∴
（舍去）
∴
∴
∴
∴
∴
（舍去）
∴
练习册系列答案
相关题目
