题目内容
【题目】如图,在平面直角坐标系xOy中,点A(﹣2,﹣2),B(0,3),C(3,3),D(4,﹣2),y是关于x的二次函数,抛物线y1经过点A、B、C,抛物线y2经过点B、C、D,抛物线y3经过点A、B、D,抛物线y4经过点A、C、D.下列判断:
①四条抛物线的开口方向均向下;
②当x<0时,至少有一条抛物线表达式中的y均随x的增大而减小;
③抛物线y1的顶点在抛物线y2顶点的上方;
④抛物线y4与y轴的交点在点B的上方.
所有正确结论的序号为_____.
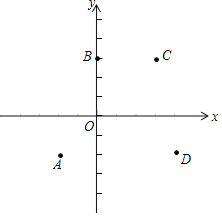
【答案】②③④.
【解析】
用待定系数法确定四条抛物线的表达式,用函数图象的性质即可求解.
解:将点A、B、C的坐标代入抛物线表达式得: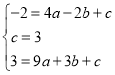 ,
,
解得: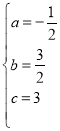 ,
,
故抛物线y1的表达式为:y1=﹣![]() x2+
x2+![]() x+3,顶点(
x+3,顶点(![]() );
);
同理可得:y2=﹣![]() x2+
x2+![]() x+3,顶点坐标为:(
x+3,顶点坐标为:(![]() ,
,![]() );
);
y3=﹣![]() x2+
x2+![]() x+3;
x+3;
y4=﹣x2+2x+6,与y轴的交点为:(0,6);
①由函数表达式知,四条抛物线的开口方向均向下,错误,不符合题意;
②当x<0时,y3随x的增大而减小,故正确,符合题意;
③由顶点坐标知,抛物线y1的顶点在抛物线y2顶点的上方,正确,符合题意;
④抛物线y4与y轴的交点(0,6)在B的上方,正确,符合题意.
故答案为:②③④.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
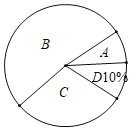
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.