��Ŀ����
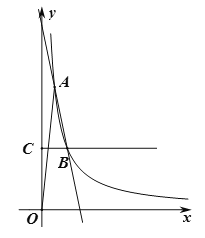
����Ŀ����֪��ֱ��y=![]() x��3��x�ᡢy��ֱ��ڵ�A��B��������y=
x��3��x�ᡢy��ֱ��ڵ�A��B��������y=![]() x2+bx+c������A��B���ҽ�x���ڵ�C��
x2+bx+c������A��B���ҽ�x���ڵ�C��
��1���������ߵĽ���ʽ��
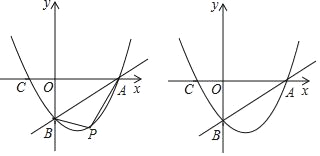
��2����PΪ��������һ�㣬�ҵ�P��AB���·������P�ĺ�����Ϊm��
������mΪ��ֵʱ����PAB��������
������PAB��������ʱ������P��x��Ĵ���PD������Ϊ��D������ֱ��PD�Ϸ���ڵ�Q��ʹ��QBCΪֱ�������Σ������ڣ�ֱ��д������������Q�������������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2��
x2��![]() x��3����2������m=3ʱ����PAB�����������ֵ��9������ֱ��PD�Ϸ���ڵ�Q��3��
x��3����2������m=3ʱ����PAB�����������ֵ��9������ֱ��PD�Ϸ���ڵ�Q��3��![]() ����3����
����3����![]() ����ʹ��QBCΪֱ�������Σ�
����ʹ��QBCΪֱ�������Σ�
��������
��1������һ�κ���ͼ���ϵ������������������A��B�����꣬�����ô���ϵ����������������ߵĽ���ʽ��
��2���ٹ���P��PD��x����D����AB�ڵ�E�����P�ĺ�����Ϊm�����P������Ϊ��m��![]() m2��
m2��![]() m��3������E��������m��
m��3������E������Ϊ��m��![]() m��3���������ɵó�PE�ij��ȣ������������ε������ʽ���ɵó�S��PAB=��m2+6m�������䷽�����ɽ����ֵ���⣻
m��3���������ɵó�PE�ij��ȣ������������ε������ʽ���ɵó�S��PAB=��m2+6m�������䷽�����ɽ����ֵ���⣻
�����ö��κ���ͼ���ϵ�����������������C�����꣬���Q������Ϊ��3��y������CQ2=��![]() ��2+y2��BC2=9+
��2+y2��BC2=9+![]() ��BQ2=9+��y+3��2���֡�QCB=90�㡢��CBQ=90������CQB=90��������������ù��ɶ������ɵó�����y�ķ��̣���֮���ɵó����ۣ�
��BQ2=9+��y+3��2���֡�QCB=90�㡢��CBQ=90������CQB=90��������������ù��ɶ������ɵó�����y�ķ��̣���֮���ɵó����ۣ�
��1����ֱ��y=![]() x��3��x�ᡢy��ֱ��ڵ�A��B��
x��3��x�ᡢy��ֱ��ڵ�A��B��
���A��������6��0������B��������0����3����
��A��6��0����B��0����3������y=![]() x2+bx+c���ã�
x2+bx+c���ã�
![]() ����ã�
����ã�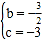 ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��![]() x��3��
x��3��
��2���ٹ���P��PD��x����D����AB�ڵ�E����ͼ1��ʾ��
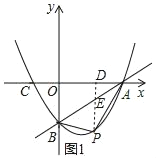
���P�ĺ�����Ϊm�����P������Ϊ��m��![]() m2��
m2��![]() m��3������E��������m��
m��3������E��������m��![]() m��3����
m��3����
��PE=![]() m��3����
m��3����![]() m2��
m2��![]() m��3��=��
m��3��=��![]() m2+2m��
m2+2m��
��S��PAB=![]() ��PE����AD+DO��=
��PE����AD+DO��=![]() ������
������![]() m2+2m����6=��m2+6m=����m��3��2+9��
m2+2m����6=��m2+6m=����m��3��2+9��
�൱m=3ʱ����PAB�����������ֵ��9��
�ڵ�y=0ʱ����![]() x2��
x2��![]() x��3=0��
x��3=0��
��ã�x1=��![]() ��x2=6��
��x2=6��
���C����������![]() ��0����
��0����
���Q��������3��y����
��CQ2=��![]() ��2+y2��BC2=9+
��2+y2��BC2=9+![]() ��BQ2=9+��y+3��2��
��BQ2=9+��y+3��2��
����QCB=90��ʱ����CQ2+BC2=BQ2��
����![]() ��2+y2+9+
��2+y2+9+![]() =9+��y+3��2��
=9+��y+3��2��
��ã�y=![]() ��
��
����CBQ=90��ʱ����BC2+BQ2=CQ2��
��9+![]() +9+��y+3��2=��
+9+��y+3��2=��![]() ��2+y2��
��2+y2��
��ã�y=��![]() ��
��
����CQB=90��ʱ����BQ2+CQ2=BC2��
����![]() ��2+y2+9+��y+3��2=9+
��2+y2+9+��y+3��2=9+![]() ��
��
�����⣮
������ʾ����ֱ��PD�Ϸ���ڵ�Q��3��![]() ����3����
����3����![]() ����ʹ��QBCΪֱ�������Σ�
����ʹ��QBCΪֱ�������Σ�