题目内容
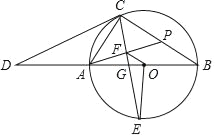
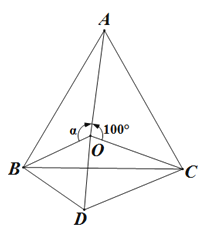
【题目】如图,点O是等边△ABC内一点,∠AOC=100°,∠AOB=α,以OB为边作等边△BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时△COD是等腰三角形?
【答案】(1)详见解析;(2)直角三角形,理由详见解析;(3)当α为100°、130°、160°时,△COD是等腰三角形.
【解析】
(1)由于 △ABC和△OBD都是等边三角形,可得BA=BC,BO=BD,由角推出∠ABO=∠CBD,即可证明△ABO≌△CBD.
(2)由△ABO≌△CBD,可得∠BDC=150°,由于∠BDO=60°,即可推出∠CDO的度数为90°,即可证明为直角三角形.
(3)分三类讨论:①要使CO=CD, ②要使OC=OD,③要使OD=CD.
(1)解:(1)∵△ABC和△OBD都是等边三角形,
∴BA=BC,BO=BD,
∵∠ABC=∠OBD=60°
∴∠ABO=∠CBD,
∴△ABO≌△CBD(SAS).
(2)直角三角形;
理由:∵△ABO≌△CBD
∴∠BDC=∠AOB=150°
又∵∠ODB=∠OBD=60°
∴∠CDO=150°-60°=90°
∴△COD是直角三角形.
(3)①要使CO=CD,需∠COD=∠CDO,
∴200°-α = α-60°,
∴α=130°;
②要使OC=OD,需∠OCD=∠CDO,
∴2(α-60°)=180°-(200°-α),
∴α=100°;
③要使OD=CD,需∠OCD=∠COD,
∴2(200°-α)=180°-(α -60°),
∴α=160°.
所以当α为100°、130°、160°时,△COD是等腰三角形.

练习册系列答案
相关题目