题目内容
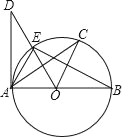
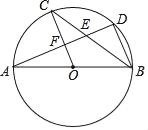
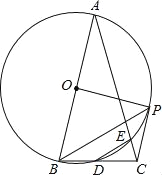
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
【答案】(1)BD=DC;理由见解析;(2)90°;(3)证明见解析;
【解析】
(1)连接AD,由圆周角定理可知∠ADB=90°,再由AB=AC可知△ABC是等腰三角形,故BD=DC;
(2)由于AD是等腰三角形ABC底边上的中线,所以∠BAD=∠CAD,故![]() =
=![]() ,进而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
,进而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°在Rt△AOG中,由∠OAG=30°,可知![]() =
=![]() ,由于
,由于![]() =
=![]() =
=![]() ,所以
,所以![]() =
=![]() ,
,![]() =
=![]() ,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是 ⊙O的切线.
,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是 ⊙O的切线.
解:(1)BD=DC.理由如下:连接AD,
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)∵AD是等腰△ABC底边上的中线,
∴∠BAD=∠CAD,
∴![]() =
=![]() ,
,
∴BD=DE.
∴BD=DE=DC,
∴∠DEC=∠DCE,
△ABC中,AB=AC,∠A=30°,
∴∠DCE=∠ABC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠DEC=75°,
∴∠EDC=180°﹣75°﹣75°=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45°,
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;
(3)设OP交AC于点G,如图,则∠AOG=∠BOP=90°,
在Rt△AOG中,∠OAG=30°,
∴![]() =
=![]() ,
,
又∵![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵∠AGO=∠CGP,
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴OP⊥PC,
∴CP是⊙O的切线;