题目内容
 已知在矩形ABCD中.
已知在矩形ABCD中.(1)设矩形的面积为6,AD=y,AB=x(0<x≤6),写出y与x的函数关系,并在直角坐标系中画出此函数的图象.
(2)如图矩形纸片ABCD,AB=4,AD=3.折叠纸片使得AD边与对角线BD重合,折痕为DG,点A落在A′处,求△A′BG的面积与矩形ABCD的面积的比是多少?
分析:(1)求出y与x的解析式,画出图形即可;
(2)根据折叠得出AD=A′D=3,∠DA′G=90°,由勾股定理求出DB=5,在Rt△A′BG中,BA′=2,BG=4-x,GA′=x,由勾股定理得出x2+22=(4-x)2,求出x=
,分别△A′BG的面积和矩形ABCD的面积即可.
(2)根据折叠得出AD=A′D=3,∠DA′G=90°,由勾股定理求出DB=5,在Rt△A′BG中,BA′=2,BG=4-x,GA′=x,由勾股定理得出x2+22=(4-x)2,求出x=
| 3 |
| 2 |
解答:(1)解:∵矩形ABCD的面积为6,AD=y,AB=x(0<x≤6),
∴y=
,图象为: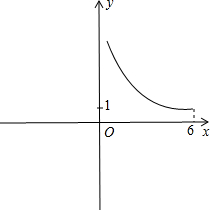
(2)解:设AG=x,则AB=4-x,
∵折叠纸片使得AD边与对角线BD重合,折痕为DG,点A落在A′处,
∴AD=A′D=3,∠DA′G=90°,
∴∠GA′B=90°,
∵四边形ABCD是矩形,
∴∠A=90°,
在△DAB中,AD=3,AB=4,由勾股定理得:DB=5,
∴A′B=5-3=2,
在Rt△A′BG中,BA′=2,BG=4-x,GA′=x,由勾股定理得:x2+22=(4-x)2,
x=
,
∴△A′BG的面积是
×A′B×GA′=
×
×2=
,
∵矩形ABCD的面积是3×4=12,
∴△A′BG的面积与矩形ABCD的面积的比是
÷12=1:8.
∴y=
| 6 |
| x |

(2)解:设AG=x,则AB=4-x,
∵折叠纸片使得AD边与对角线BD重合,折痕为DG,点A落在A′处,
∴AD=A′D=3,∠DA′G=90°,
∴∠GA′B=90°,
∵四边形ABCD是矩形,
∴∠A=90°,
在△DAB中,AD=3,AB=4,由勾股定理得:DB=5,
∴A′B=5-3=2,
在Rt△A′BG中,BA′=2,BG=4-x,GA′=x,由勾股定理得:x2+22=(4-x)2,
x=
| 3 |
| 2 |
∴△A′BG的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∵矩形ABCD的面积是3×4=12,
∴△A′BG的面积与矩形ABCD的面积的比是
| 3 |
| 2 |
点评:本题考查了矩形的性质,勾股定理,折叠性质,反比例函数等知识点,主要考查学生的计算能力和动手操作能力.

练习册系列答案
相关题目
 ,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).

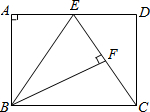 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.