题目内容
如图,两条公路AB,CD(均视为直线).东西向公路CD段限速,规定最高行驶速度不能越过60千米/时,并在南北向公路离该公路100米的A处没置了一个监测点.已知点C在A的北偏西60°方向上,点D在A的北偏东45°方向上.(1)经监测,一辆汽车从点C匀速行驶到点D所的时间是15秒,请通过计算,判断该汽车在这段限速路上是否超速?(参考数据:
 =1.732)
=1.732)(2)若一辆大货车在限速路上由D处向西行驶,一辆小汽车在南北向公路上由A处向北行驶,设两车同时开出且小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?

【答案】分析:(1)判断是否超速就是求DC的长,然后比较;
(2)求两车在匀速行驶过程中的最近距离可以转化为求函数的最值问题,或转化为利用配方法求最值的问题.
解答:解:(1)由题意知∠BAD=45°,∠CAB═60°,
在Rt△AOD中,OD=OA=100米,在Rt△AOC中,OC=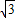 OA=100
OA=100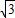 米,
米,
∴DC=(100+100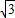 )米,
)米,
实际速度v=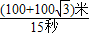 ≈18.2米/秒=65.52千米/小时>60千米/小时,
≈18.2米/秒=65.52千米/小时>60千米/小时,
∴超速.
(2)∵两车同时开出且小汽车的速度是大货车速度的2倍,
∴当大货车由B开出x米时,小汽车由A开出了2x米,
两车之间的距离S=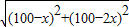 =
=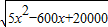 =
=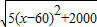
∴当x=60时,S取得最小值,为20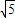 米.
米.
点评:本题考查解直角三角形的应用,属于实际应用类题目,从复杂的实际问题中整理出直角三角形是解决此类问题的关键.
(2)求两车在匀速行驶过程中的最近距离可以转化为求函数的最值问题,或转化为利用配方法求最值的问题.
解答:解:(1)由题意知∠BAD=45°,∠CAB═60°,
在Rt△AOD中,OD=OA=100米,在Rt△AOC中,OC=
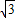 OA=100
OA=100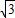 米,
米,∴DC=(100+100
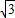 )米,
)米,实际速度v=
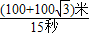 ≈18.2米/秒=65.52千米/小时>60千米/小时,
≈18.2米/秒=65.52千米/小时>60千米/小时,∴超速.
(2)∵两车同时开出且小汽车的速度是大货车速度的2倍,
∴当大货车由B开出x米时,小汽车由A开出了2x米,
两车之间的距离S=
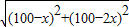 =
=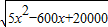 =
=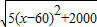
∴当x=60时,S取得最小值,为20
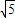 米.
米.点评:本题考查解直角三角形的应用,属于实际应用类题目,从复杂的实际问题中整理出直角三角形是解决此类问题的关键.

练习册系列答案
相关题目
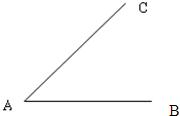 22、如图,两条公路AB,AC相交于点A,现要建个车站D,使得D到A村和B村的距离相等,并且到公路AB、AC的距离也相等,请在图中画出车站的位置.
22、如图,两条公路AB,AC相交于点A,现要建个车站D,使得D到A村和B村的距离相等,并且到公路AB、AC的距离也相等,请在图中画出车站的位置. 小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?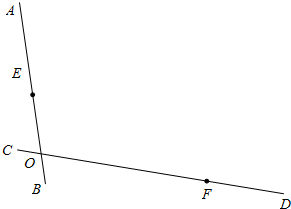 如图,两条公路AB、CD相交于O,小明家在公路AB边的点E处,小亮家在公路CD与公路MN的十字路口F处(公路MN与公路AB平行),两个好朋友约好在公路MN上的公园P见面,且公园P到小明家E和到小亮家F的距离相等.请用直尺和圆规在原图上确定公园P的位置(不写已知、求作和结论,只需要保留作图痕迹).
如图,两条公路AB、CD相交于O,小明家在公路AB边的点E处,小亮家在公路CD与公路MN的十字路口F处(公路MN与公路AB平行),两个好朋友约好在公路MN上的公园P见面,且公园P到小明家E和到小亮家F的距离相等.请用直尺和圆规在原图上确定公园P的位置(不写已知、求作和结论,只需要保留作图痕迹).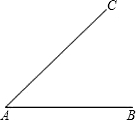 如图,两条公路AB,AC相交于点A,现要建个车站D,使得D到A村和B村的距离相等,并且到公路AB、AC的距离也相等,请在图中画出车站的位置.
如图,两条公路AB,AC相交于点A,现要建个车站D,使得D到A村和B村的距离相等,并且到公路AB、AC的距离也相等,请在图中画出车站的位置.