Question

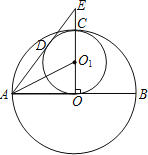
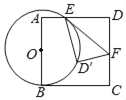
【题目】如图，O是正方形ABCD边上一点，以O为圆心，OB为半径画圆与AD交于点E，过点E作⊙O的切线交CD于F，将△DEF沿EF对折，点D的对称点D'恰好落在⊙O上．若AB＝6，则OB的长为_____．

Answer 1

【答案】

【解析】

连接OE、OD′，作OH⊥ED′于H，通过证得AEO≌△HEO（AAS），AE＝EH＝ED＝2，设OB＝OE＝x．则AO＝6﹣x，根据勾股定理得x2＝22+（6﹣x）2，解方程即可求得结论．

解：连接OE、OD′，作OH⊥ED′于H，

∴EH＝D′H＝ED′

∵ED′＝ED，

∴EH＝ED，

∵四边形ABCD是正方形，

∴∠A＝90°，AB＝AD＝6，

∵EF是⊙O的切线，

∴OE⊥EF，

∴∠OEH+∠D′EF＝90°，∠AEO+∠DEF＝90°，

∵∠DEF＝∠D′EF，

∴∠AEO＝∠HEO，

在△AEO和△HEO中

∴△AEO≌△HEO（AAS），

∴AE＝EH＝ED，

∴ 设OB＝OE＝x．则AO＝6﹣x，

在Rt△AOE中，x2＝22+（6﹣x）2，

解得：x＝，

∴OB＝，

故答案为:．