题目内容
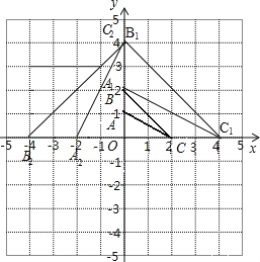
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为A(0,1),B(0,2),C(2,0).
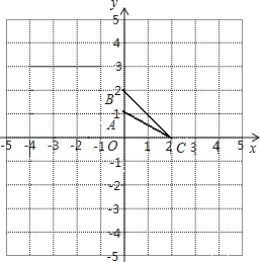
(1)请画出△A1BlCl,使△A1BlCl与△ABC是以O为位似中心的位似图形,且位似比为2:1,并使这两个三角形在位似中心同侧;
(2)将△A1BlC1绕O点逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并求出线段A1B1在旋转过程中所扫过的图形面积.
【答案】(1)如图,△A1B1C1为所作;见解析;(2)如图,△A2B2C2为所作;见解析;线段A1B1在旋转过程中所扫过的图形面积为3π.
【解析】
(1)把A、B、C点的横纵坐标乘以2得到点A1、B1、C1的坐标,然后描点即可;
(2)利用旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,从而得到△A2B2C2;然后利用扇形的面积差去计算线段A1B1在旋转过程中所扫过的图形面积.
(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;线段A1B1在旋转过程中所扫过的图形面积=![]() =3π.
=3π.

【题目】已知二次函数y=﹣2x2﹣4x+6.
(1)用配方法求出函数的顶点坐标;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()