ћвƒњƒЏ»Ё
°Њћвƒњ°њ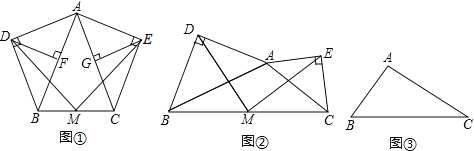
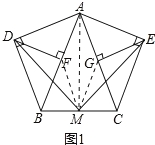
»зЌЉҐў£ђ‘Џµ»—ь°чABC÷–£ђAB=AC£ђЈ÷±р“‘ABЇЌACќ™–±±я£ђѕт°чABCµƒЌв≤а„чµ»—ь÷±љ«»эљ«–ќ£ђ»зЌЉҐўЋщ Њ£ђ∆д÷–£ђDF°ЌAB”ЏµгF£ђEG°ЌAC”ЏµгG£ђM «BCµƒ÷–µг£ђЅђљ”MD£ђME£ђMF£ђMG£Ѓ‘тѕ¬Ѕ–љб¬џ’э»Јµƒ «__________£®ћо–і–тЇ≈£©
ҐўЋƒ±я–ќAFMG «Ѕв–ќ£їҐЏ°чDFMЇЌ°чEGMґЉ «µ»—ь»эљ«–ќ£їҐџMD=ME£їҐ№MD°ЌME£Ѓ
£®2£© э—ІЋЉњЉ£Ї
»зЌЉҐЏ£ђ‘Џ»ќ“в°чABC÷–£ђЈ÷±р“‘ABЇЌACќ™–±±я£ђѕт°чABCµƒЌв≤а„чµ»—ь÷±љ«»эљ«–ќ£ђM «BCµƒ÷–µг£ђЅђљ”MDЇЌME£ђ‘тMD”лMEЊя”–‘х—щµƒ эЅњЇЌќї÷√єЎѕµ£њ«лЄш≥ц÷§√чєэ≥ћ£Ѓ
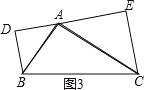
£®3£©ја±»ћљЊњ£Ї»зЌЉҐџRt°чABC÷–£ђ–±±яBC=10£ђAB=6£ђЈ÷±р“‘AB°ҐACќ™–±±я„чµ»—ь÷±љ«»эљ«–ќABDЇЌACE£ђ«л÷±љ”–і≥цDEµƒ≥§£Ѓ
°Њір∞Є°њ£®1£©ҐўҐЏҐџҐ№£ї£®2£©![]() ÷§√чЉыљвќц£ї£®3£©DEµƒ≥§ќ™£Ї
÷§√чЉыљвќц£ї£®3£©DEµƒ≥§ќ™£Ї![]() їт
їт![]() ,
,![]() .
.
°Њљвќц°њ
‘ћвЈ÷ќц£Ї£®1£©”…ћхЉюњ…“‘Ќ®єэ»эљ«–ќ»Ђµ»ЇЌ÷бґ‘≥∆µƒ–‘÷ £ђ÷±љ«»эљ«–ќ–±±я…ѕµƒ÷–ѕя–‘÷ “‘Љ∞Ћƒµгє≤‘≤Љіњ…µ√≥цљб¬џ£ї
£®2£©»°AB°ҐACµƒ÷–µгF°ҐG£ђЅђљ”DF£ђMF£ђEG£ђMG£ђЄщЊЁ»эљ«–ќµƒ÷–ќїѕяµƒ–‘÷ ЇЌµ»—ь÷±љ«»эљ«–ќµƒ–‘÷ ЊЌњ…“‘µ√≥цЋƒ±я–ќAFMG «∆љ––Ћƒ±я–ќ£ђі”ґшµ√≥ц°чDFM°’°чMGE£ђЄщЊЁ∆д–‘÷ “‘Љ∞ЄчЄцљ«÷ЃЉдµƒєЎѕµЉіњ…µ√≥цљб¬џ£ї
£®3£©Ј÷Ћƒ÷÷«йњц£ђҐўµ»—ь÷±љ«»эљ«–ќABDЇЌACEґЉ‘ЏRt°чABCЌв≤а£ђҐЏµ»—ь÷±љ«»эљ«–ќABDЇЌACEґЉ‘ЏRt°чABCƒЏ≤а£ђҐџµ»—ь÷±љ«»эљ«–ќABDЇЌACE“їЄцRt°чABCЌв≤а£ђҐ№µ»—ь÷±љ«»эљ«–ќABDЇЌACE,“їЄц‘ЏRt°чABCЌв≤а£ђ“їЄц‘Џµ»—ь÷±љ«»эљ«–ќABDЇЌACEґЉ‘ЏRt°чABCƒЏ≤аЈ÷±р«у≥цDEµƒ≥§ґ»Љіњ…£Ѓ
‘ћвљвќц£Ї£®1£©°я![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]() °я‘Џ
°я‘Џ![]() ЇЌ
ЇЌ![]() ÷–£ђ
÷–£ђ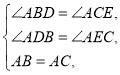
![]()
![]()
![]() ”ЏµгF£ђ
”ЏµгF£ђ![]() ”ЏµгG£ђ
”ЏµгG£ђ![]()
![]()
![]()
![]() °а
°а![]() ЇЌ
ЇЌ![]() ґЉ «µ»—ь»эљ«–ќ£ђє ҐЏ’э»Ј£ї °яM «BCµƒ÷–µг£ђ°а
ґЉ «µ»—ь»эљ«–ќ£ђє ҐЏ’э»Ј£ї °яM «BCµƒ÷–µг£ђ°а ![]()
![]() °а
°а![]()
![]() Љі
Љі![]() ‘Џ
‘Џ![]() ЇЌ
ЇЌ![]() ÷–£ђ
÷–£ђ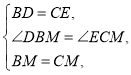
![]()
![]() є Ґџ’э»Ј£їЅђљ”AM°ҐFM°ҐGM£ђ»зЌЉ1Ћщ Њ£Ї
є Ґџ’э»Ј£їЅђљ”AM°ҐFM°ҐGM£ђ»зЌЉ1Ћщ Њ£Ї
![]() M «BCµƒ÷–µг£ђ
M «BCµƒ÷–µг£ђ![]()
![]()
![]()
![]()
![]()
![]() °аЋƒ±я–ќAFMG «Ѕв–ќ£ђє Ґў’э»Ј£ї
°аЋƒ±я–ќAFMG «Ѕв–ќ£ђє Ґў’э»Ј£ї![]() M «BCµƒ÷–µг£ђ
M «BCµƒ÷–µг£ђ![]()
![]()
![]() °аЋƒ±я–ќADBMЋƒµгє≤‘≤£ђ
°аЋƒ±я–ќADBMЋƒµгє≤‘≤£ђ![]() °яAM «ґ‘≥∆÷б,
°яAM «ґ‘≥∆÷б,![]()
![]()
![]() є Ґ№’э»Ј£ђє ір∞Єќ™£ЇҐўҐЏҐџҐ№£ї
є Ґ№’э»Ј£ђє ір∞Єќ™£ЇҐўҐЏҐџҐ№£ї
£®2£©![]() јн”…»зѕ¬£Ї»°AB°ҐACµƒ÷–µгF°ҐG£ђЅђљ”DF£ђMF£ђEG£ђMG£ђ»зЌЉ2Ћщ Њ£Ї
јн”…»зѕ¬£Ї»°AB°ҐACµƒ÷–µгF°ҐG£ђЅђљ”DF£ђMF£ђEG£ђMG£ђ»зЌЉ2Ћщ Њ£Ї
![]() °я°чABDЇЌ°чAEC «µ»—ь÷±љ«»эљ«–ќ£ђ
°я°чABDЇЌ°чAEC «µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]()
![]()
![]() °яM «BCµƒ÷–µг£ђ
°яM «BCµƒ÷–µг£ђ![]() °аЋƒ±я–ќAFMG «∆љ––Ћƒ±я–ќ£ђ
°аЋƒ±я–ќAFMG «∆љ––Ћƒ±я–ќ£ђ![]()
![]()
![]()
![]()
![]() °я‘Џ
°я‘Џ![]() ЇЌ
ЇЌ![]() ÷–£ђ
÷–£ђ
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)![]() ÷–£ђ–±±яBC=10£ђAB=6£ђ°аAC=8£ђ
÷–£ђ–±±яBC=10£ђAB=6£ђ°аAC=8£ђ![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]() Ј÷Ћƒ÷÷«йњц£ђҐў»зЌЉ3£ђ
Ј÷Ћƒ÷÷«йњц£ђҐў»зЌЉ3£ђ![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]()
![]() °аD£ђA£ђE»эµгє≤ѕя£ђ
°аD£ђA£ђE»эµгє≤ѕя£ђ![]() ҐЏ»зЌЉ4£ђ
ҐЏ»зЌЉ4£ђ![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]() °аµгA£ђD£ђEє≤ѕя£ђ
°аµгA£ђD£ђEє≤ѕя£ђ![]() Ґџ»зЌЉ5£ђ
Ґџ»зЌЉ5£ђ![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]()
![]()
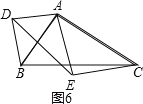
![]() Ґ№»зЌЉ6£ђ
Ґ№»зЌЉ6£ђ![]() ЇЌ
ЇЌ![]() «µ»—ь÷±љ«»эљ«–ќ£ђ
«µ»—ь÷±љ«»эљ«–ќ£ђ![]()
![]()
![]()
![]() „џ…ѕЋщ ц£ЇDEµƒ≥§ќ™£Ї
„џ…ѕЋщ ц£ЇDEµƒ≥§ќ™£Ї![]() їт
їт![]() ,
,![]() .
.