题目内容
【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:(1)BD=AE.(2)若线段AD=5,AB=17,求线段ED的长。

【答案】(1)、证明过程见解析;(2)、13.
【解析】试题分析:(1)、根据等腰直角三角形的性质得出AC=BC,CD=CE,∠ACD=∠DCE=90°,从而说明∠ACE=∠BCD,然后根据SAS判定三角形全等,从而得到BD=AE;(2)、根据题意得出BD的长度,根据全等从而得到AE的长度以及∠EAD为直角,然后利用Rt△AED的勾股定理求出DE的长度.
试题解析:(1)、∵△ABC和△ECD都是等腰直角三角形, ∴AC=BC,CD=CE, ∵∠ACD=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD, ∴∠ACE=∠BCD,
在△ACE和△BCD中,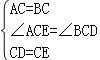 , ∴△ACE≌△BCD(SAS), ∴BD=AE.
, ∴△ACE≌△BCD(SAS), ∴BD=AE.
(2)、∵AD="5," AB="17," ∴BD=17-5=12 ∵△ABC是等腰直角三角形
∴∠B=45°由(1)可知△ACE≌△BCD ∴∠EAC=∠B=45° AE=BD=7
∴∠EAD=90° ∴ED=![]()

练习册系列答案
相关题目