题目内容
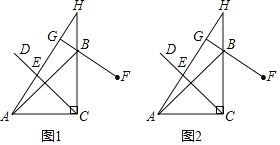
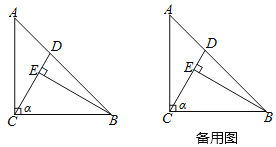
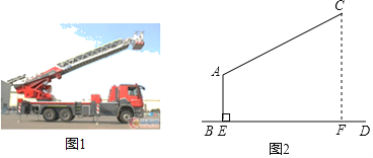
【题目】图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂AC是可伸缩的，其转动点A距离地面BD的高度AE为3.5m．当AC长度为9m，张角∠CAE为112°时，求云梯消防车最高点C距离地面的高度CF．（结果精确到0.1m，参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40．）
【答案】CF≈6.8m．
【解析】
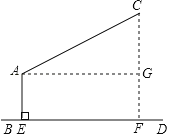
如图，作AG⊥CF于点G，易得四边形AEFG为矩形，则FG＝AE＝3.5m，∠EAG＝90°，再计算出∠GAC＝28°，则在Rt△ACG中利用正弦可计算出CG，然后计算CG+GF即可．
如图，作AG⊥CF于点G，
∵∠AEF＝∠EFG＝∠FGA＝90°，
∴四边形AEFG为矩形，
∴FG＝AE＝3.5m，∠EAG＝90°，
∴∠GAC＝∠EAC﹣∠EAG＝112°﹣90°＝22°，
在Rt△ACG中，sin∠CAG＝
，
∴CG＝ACsin∠CAG＝9sin22°≈9×0.37＝3.33m，
∴CF＝CG+GF＝3.33+3.5≈6.8m．
练习册系列答案
相关题目
