题目内容
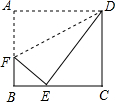
如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③S△DOG=S四边形EFOG;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )

| A.2 | B.3 | C.4 | D.5 |

∵四边形ABCD是正方形,
∴∠DAC=∠ADB=∠ABD=45°,
由折叠的性质可得:∠ADE=∠FDE=
∠ADB=22.5°,
则∠AEG=90°-∠ADE=67.5°,∠AGE=∠ADE+∠DAC=22.5°+45°=67.5°,
∵∠AGE=∠AEG=67.5°,
∴AE=AG,即①正确;
设EF=x,则AE=x,BE=
EF=
x,AB=AE+BE=(
+1)x,
tan∠AGE=tan∠AEG=
=
=
+1.即②错误;
∵AB=(
+1)x,
∴AO=(1+
)x,OG=AO-AG=AO-AE=
x,
易得△DOG∽△DFE,
∵
=(
)2=
,
∴可得S△DOG=S四边形EFOG,即③正确;
∵∠AGE=∠FGE(折叠的性质),∠AGE=∠AEG(①已证),
∴∠FGE=∠AEG,
∴GF∥AB,
又∵BF=EF(等腰直角三角形的性质)=AE=AG,
∴四边形ABFG为等腰梯形,即④正确;
由上面的解答可得:AE=
x,OG=
x,
故可得BE=2OG,即⑤正确.
综上可得:①③④⑤正确,共4个.
故选C.
∴∠DAC=∠ADB=∠ABD=45°,
由折叠的性质可得:∠ADE=∠FDE=
| 1 |
| 2 |
则∠AEG=90°-∠ADE=67.5°,∠AGE=∠ADE+∠DAC=22.5°+45°=67.5°,
∵∠AGE=∠AEG=67.5°,
∴AE=AG,即①正确;
设EF=x,则AE=x,BE=
| 2 |
| 2 |
| 2 |
tan∠AGE=tan∠AEG=
| AD |
| AE |
| AB |
| AE |
| 2 |
∵AB=(
| 2 |
∴AO=(1+
| ||
| 2 |
| ||
| 2 |
易得△DOG∽△DFE,
∵
| S△DOG |
| S△DFE |
| OG |
| EF |
| 1 |
| 2 |
∴可得S△DOG=S四边形EFOG,即③正确;
∵∠AGE=∠FGE(折叠的性质),∠AGE=∠AEG(①已证),
∴∠FGE=∠AEG,
∴GF∥AB,
又∵BF=EF(等腰直角三角形的性质)=AE=AG,
∴四边形ABFG为等腰梯形,即④正确;
由上面的解答可得:AE=
| 2 |
| ||
| 2 |
故可得BE=2OG,即⑤正确.
综上可得:①③④⑤正确,共4个.
故选C.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
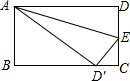


 与线段CF,AF相交于P,M.
与线段CF,AF相交于P,M.