题目内容
折叠长方形ABCD的一边AD，点D落在BC边的D′处，AE是折痕，已知CD=6cm，CD′=2cm，则AD的长为______．
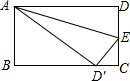
∵折叠长方形ABCD的一边AD，点D落在BC边的D′处，
∴AD=AD′，设AD=xcm，
则BD′=（x-2）cm，
在Rt△ABD′中，AD′2=AB2+D′B2，
即x2=62+（x-2）2，
解得x=10，
即AD的长为：10cm．
故答案为：10cm．
∴AD=AD′，设AD=xcm，
则BD′=（x-2）cm，
在Rt△ABD′中，AD′2=AB2+D′B2，
即x2=62+（x-2）2，
解得x=10，
即AD的长为：10cm．
故答案为：10cm．
练习册系列答案
相关题目
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．
