题目内容
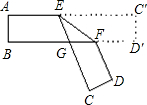
如图，在矩形ABCD中，AB=3，BC=9，把矩形ABCD沿对角线BD折叠，使点C与点F重合，BF交AD于点M，过点C作CE⊥BF于点E，交AD于点G，则MG的长=______．
设AM长为x．
在Rt△ABM中，AB2+x2=BM2，BM=MD=9-x
则32+x2=（9-x）2，
解得x=4，
BM=MD=9-x=5，
∵△GEM∽△DFM，△GDC∽△GEM，
∴△GDC∽△DFM，
∴CD：FM=GD：DF，即3：（9-5）=GD：3
解得GD=
，
所以MG=MD-GD=5-
=
．
故答案为：
．
在Rt△ABM中，AB2+x2=BM2，BM=MD=9-x
则32+x2=（9-x）2，
解得x=4，
BM=MD=9-x=5，
∵△GEM∽△DFM，△GDC∽△GEM，
∴△GDC∽△DFM，
∴CD：FM=GD：DF，即3：（9-5）=GD：3
解得GD=
| 9 |
| 4 |
所以MG=MD-GD=5-
| 9 |
| 4 |
| 11 |
| 4 |
故答案为：
| 11 |
| 4 |
练习册系列答案
相关题目
，则该车的牌照号码是______．
