题目内容
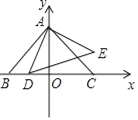
【题目】如图，在平面直角坐标系中，点A（0，2），B（﹣2，0），点D是x轴上一个动点，以AD为一直角边在一侧作等腰直角三角形ADE，∠DAE=90°，若△ABD为等腰三角形时点E的坐标为___________．
【答案】（2，2）或（2，4）或（2，2
）或（2，﹣2
）．
【解析】连接EC．
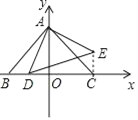
∵∠BAC=∠DAE=90°，
∴∠BAD=∠CAE，
在△BAD和△ACE中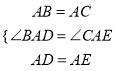
，
∴△ABD≌△ACE，
∴BD=EC．∠ABD=∠ACE=45°，
∵∠ACB=45°，
∴∠ECD=90°，
∴点E在过点C垂直x轴的直线上，且EC=DB，
①当DB=DA时，点D与O重合，BD=OB=2，此时E（2，2）．
②当AB=AD时，BD=CE=4，此时E（2，4）．
③当BD=AB=2
时，E（2，2
）或（2，﹣2
），
故答案为（2，2）或（2，4）或（2，2
）或（2，﹣2
）．
练习册系列答案
相关题目
【题目】某校篮球队13名同学的身高如下表：
身高（cm） | 175 | 180 | 182 | 185 | 188 |
人数（个） | 1 | 5 | 4 | 2 | 1 |
则该校篮球队13名同学身高的众数和中位数分别是（ ）
A.182，180
B.180，180
C.180，182
D.188，182
