Question

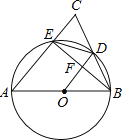
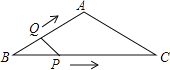
【题目】如图，△ABC内接于⊙O，且AB＝AC，延长BC至点D，使CD＝CA，连接AD交⊙O与点E，连接BE，CE.

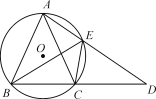
(1)求证：△ABE≌△CDE；

(2)填空：

①当∠ABC的度数为______时，四边形AOCE是菱形；

②若AE＝，AB＝2，则DE的长为______．

Answer 1

【答案】(1)见解析；(2)①60°；②

【解析】

（1）由AB＝AC，CD=CA得出AB=CD，再根据圆内接四边形的性质和圆周角的性质可知，∠CED＝∠AEB从而可证

（2）①根据菱形的性质可知为等边三角形，进而可推出

②由可得进而可可，再利用相似三角形的性质可知,从而可求.

（1）证明：∵AB＝AC，CD=CA

∴∠ABC＝∠ACB，AB=CD

.∵四边形ABCE是圆内接四边形

∴∠CED＝∠AEB.

在和中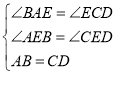

（2）①当时，四边形AOCE是菱形

理由如下：连接AO,CO,OE，如下图

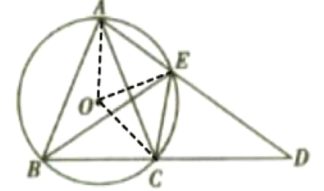
∵四边形AOCE是菱形

∴

又

∴为等边三角形

②由可得

即