题目内容
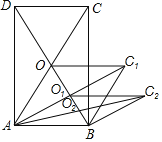
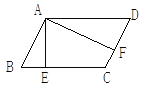
【题目】如图，已知□ABCD中，AE⊥BC，AF⊥DC，BC∶CD= 3∶2，AB=EC，则∠EAF=（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】分析：设BC=3x，则CD=2x，由平行四边形的性质得出AB=CD=2x，AB∥DC，由已知条件得出∠BAF=90°，EC=2x，得出BE=
AB，证出∠BAE=30°，即可得出∠EAF的度数
详解：设BC=3x，则CD=2x，
∵四边形ABCD是平行四边形，
∴AB=CD=2x，AB∥DC，
∵AE⊥BC，AF⊥DC，
∴∠AEB=90°，AF⊥AB，
∴∠BAF=90°，
∵AB=EC，
∴EC=2x，
∴BE=BC=EC=x=AB，
∴∠BAE=30°，
∴∠EAF=90°-30°=60°，
故选B．
练习册系列答案
相关题目
