题目内容
【题目】建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如下表:
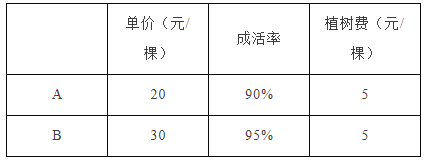
设购买A种树苗x棵,绿化村道的总费用为y元.解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
【答案】(1)y=10x+35000(x≤1000);(2)总费用需要30000元;(3)最多可购买B种树苗600棵.
【解析】
(1)设购买A种树苗x棵,则购买B种树苗(1000x)棵,根据总费用=(购买A种树苗的费用+种植A种树苗的费用)+(购买B种树苗的费用+种植B种树苗的费用),即可求出y(元)与x(棵)之间的函数关系式;
(2)根据这批树苗种植后成活了925棵,列出关于x的方程,解方程求出此时x的值,再代入(1)中的函数关系式中即可计算出总费用;
(3)根据绿化村道的总费用不超过31000元,列出关于x的一元一次不等式,求出x的取值范围,即可求解.
解:(1)设购买A种树苗x棵,则购买B种树苗(1000x)棵,由题意,得
y=(20+5)x+(30+5)(1000x)=10x+35000(x≤1000);
(2)由题意,可得0.90x+0.95(1000x)=925,
解得x=500.
当x=500时,y=10×500+35000=30000,
即绿化村道的总费用需要30000元;
(3)由(1)知购买A种树苗x棵,B种树苗(1000x)棵时,总费用y=10x+35000,
由题意,得10x+35000≤31000,
解得x≥400,
所以1000x≤600,
故最多可购买B种树苗600棵.